题目内容
数列{an}的前n项和记为Sn,点(n,Sn)在曲线f(x)=x2-4x(x∈N*)上.
(1)求数列{an}的通项公式;
(2)设bn=an•2n-1,求数列{bn}的前n项和Tn的值.
(1)求数列{an}的通项公式;
(2)设bn=an•2n-1,求数列{bn}的前n项和Tn的值.
考点:数列的求和,等差数列的性质
专题:点列、递归数列与数学归纳法
分析:(1)由题意可得Sn=n2-4n(n∈N*),利用递推公式an=Sn-Sn-1,可求.
(2)由bn=an•2n-1,得bn=(2n-5)•2n-1,利用错位相减法可求数列的和.
(2)由bn=an•2n-1,得bn=(2n-5)•2n-1,利用错位相减法可求数列的和.
解答:
解:(1)由点(n,Sn)在曲线f(x)=x2-4x上(x∈N+)知Sn=n2-4n(n∈N*)
当n≥2时an=Sn-Sn-1=n2-4n-[(n-1)2-4(n-1)]=2n-5;
当n=1时,a1=S1=-3,满足上式;
∴数列{an}的通项公式为an=2n-5(n∈N)
(2)∵bn=an•2n-1,an=2n-5(n∈N)
∴bn=(2n-5)•2n-1,
∴Tn=-3×20+(-1)×21+1×22+…+(2n-5)×2n-1①
上式两边乘以2,得
2Tn=-3×21+(-1)×22+1×23+…+(2n-5)×2n②
①-②得,
解得,Tn=(2n-7)×2n+7.
当n≥2时an=Sn-Sn-1=n2-4n-[(n-1)2-4(n-1)]=2n-5;
当n=1时,a1=S1=-3,满足上式;
∴数列{an}的通项公式为an=2n-5(n∈N)
(2)∵bn=an•2n-1,an=2n-5(n∈N)
∴bn=(2n-5)•2n-1,
∴Tn=-3×20+(-1)×21+1×22+…+(2n-5)×2n-1①
上式两边乘以2,得
2Tn=-3×21+(-1)×22+1×23+…+(2n-5)×2n②
①-②得,
|
解得,Tn=(2n-7)×2n+7.
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,错位相减求解数列的和是数列求和的重要方法,要注意掌握.

练习册系列答案
相关题目
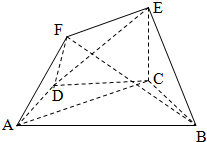 如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=
如图,在多面体ABCDEF中,底面ABCD是梯形,且满足AD=DC=CB=