题目内容
(1)计算:2log2
-(
)-
+lg
+(
-1)lg1
(2)已知x
+x-
=3,求
的值.
| 1 |
| 4 |
| 8 |
| 27 |
| 2 |
| 3 |
| 1 |
| 100 |
| 2 |
(2)已知x
| 1 |
| 2 |
| 1 |
| 2 |
| x2+x-2-2 |
| x+x-1-3 |
分析:(1)利用指数幂和对数的运算性质即可得出;
(2)由x
+x-
=3,经过平方可得x+x-1,x2+x-2,进而得到.
(2)由x
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)原式=2log22-2-[(
)-3]-
-lg10-2+(
-1)0
=
-
-2+1=-3.
(2)∵(x
+x-
)2=x+x-1+2=9,
∴x+x-1=7,
∴(x+x-1)2=x2+x-2+2=49,化为x2+x-2=47.
原式=
=
.
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
=
| 1 |
| 4 |
| 9 |
| 4 |
(2)∵(x
| 1 |
| 2 |
| 1 |
| 2 |
∴x+x-1=7,
∴(x+x-1)2=x2+x-2+2=49,化为x2+x-2=47.
原式=
| 47-2 |
| 7-3 |
| 45 |
| 4 |
点评:本题考查了指数幂和对数的运算性质、完全平方公式,属于基础题.

练习册系列答案
相关题目
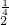
 -1)0+(
-1)0+( )
)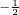 +(
+( )
)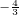 .
.