题目内容
A(5,y1),B(x2,y2),C(100,y3)是双曲线 上三点,O是坐标原点.若
上三点,O是坐标原点.若 ,且AC的斜率为
,且AC的斜率为 ,则BC的斜率为 .
,则BC的斜率为 .
【答案】分析:根据双曲线的对称性可知A,B关于原点对称,设出A,B和C的坐标,把A,C点坐标代入双曲线方程可求得直线AC和直线AB的斜率之积,进而求得a和b的关系,进而根据a,b求得BC的斜率.
解答:解:∵ ,∴A,B关于原点对称,
,∴A,B关于原点对称,
为方便运算,不妨设A,B,C三点的坐标分别为 (x1,y1),(-x1,-y1),(x3,y3 ),
由 kCA•kCB= •
• =
= =
= ①.
①.
又 ,
, ,
,
∴ ,
,
 ②,
②,
由①②可得 =kCA•kCB,
=kCA•kCB,
∵AC的斜率为 ,
,
则BC的斜率为:
故答案为: .
.
点评:本题主要考查双曲线的几何性质,考查点差法,关键是设点代入化简,应注意双曲线几何量之间的关系.
解答:解:∵
 ,∴A,B关于原点对称,
,∴A,B关于原点对称,为方便运算,不妨设A,B,C三点的坐标分别为 (x1,y1),(-x1,-y1),(x3,y3 ),
由 kCA•kCB=
 •
• =
= =
= ①.
①.又
 ,
, ,
,∴
 ,
, ②,
②,由①②可得
 =kCA•kCB,
=kCA•kCB,∵AC的斜率为
 ,
,则BC的斜率为:

故答案为:
 .
.点评:本题主要考查双曲线的几何性质,考查点差法,关键是设点代入化简,应注意双曲线几何量之间的关系.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2007•广州一模)函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(2007•广州一模)函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.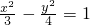 上三点,O是坐标原点.若
上三点,O是坐标原点.若 ,且AC的斜率为
,且AC的斜率为 ,则BC的斜率为________.
,则BC的斜率为________. 上三点,O是坐标原点.若
上三点,O是坐标原点.若 ,且AC的斜率为
,且AC的斜率为 ,则BC的斜率为 .
,则BC的斜率为 .