Question

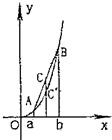
在函数y=lgx（x＞1）的图象有A、B、C三点，横坐标分别为：m，m+2，m+4，
（1）若△ABC的面积为S，求S=f（m）的解析式；
（2）求S=f（m）的最大值；
（3）若a、b、c和lga、lgb、lgc分别是两个三角形的三条边，且a、b、c互不相等，那么这两个三角形能否相似？说明理由．

Answer 1

（1）过分别过A，B，C作AA₁⊥x轴，BB₁⊥x轴，CC₁⊥x轴分别交x轴于A₁，B₁，C₁
则S=S梯形AA₁B₁B+S梯形BB₁C₁D-S梯形AA₁C₁D
=

1

2

[lgm+lg（m+2）]×2+

1

2

[lg（m+2）+lg（m+4）]×2-

1

2

[lgm+lg（m+4）]×4=2lg（m+2）-lg（m+4）-lgm（m≥1）
∴S_△ABC=lg

(m+2)2

m(m+4)

=lg（1+

4

m2+4m

），（m≥1）
（2）S_△ABC=lg（1+

4

(m+2)2-4

）这个函数可以看做复合函数
因为S=lgx是增函数，所以要是S最大，只要函数x=1+

4

(m+2)2-4

最大即可
在[1，+∞）?S_mgx=f（1）=lg

9

5

=2lg3-lg5；
（3）不相似．依题意，设a＜b＜c，则有lga＜lgb＜lgc，若相似，则有

a

lga

=

b

lgb

=

c

lgc

=k，k为常数
?a、b、c为方程x=klgx的三个根．
而曲线y=x与y=klgx至多有两个交点，所以产生矛盾，因而这两个三角形不相似．