题目内容
曲线在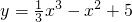 在x=1处的切线的倾斜角为________.
在x=1处的切线的倾斜角为________.
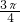
分析:利用求导法则求出曲线解析式的导函数,把x=1代入求出对应的导函数值即为切线方程的斜率,根据直线斜率与倾斜角的正切值相等,可得出倾斜角的正切值,根据倾斜角的范围,利用特殊角的三角函数值即可求出倾斜角的度数.
解答:求导得:y′=x2-2x,
把x=1代入导函数得:y′|x=1=1-2=-1,
∴切线方程的斜率k=tanα=-1(设α为切线的倾斜角),
又α∈[0,π),∴α=
 .
.故答案为:

点评:此题考查了导数的几何意义,特殊角的三角函数值以及直线的倾斜角,掌握切点横坐标对应的导函数值为切线方程的斜率,以及直线的斜率等于直线倾斜角的正切值是解本题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y= =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=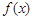 =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=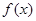 ≤2x-2.
≤2x-2. =x+ax2+blnx,曲线y=
=x+ax2+blnx,曲线y=