题目内容
已知函数f(x)=x+sinx.
(1)设P,Q是函数f(x)的图象上相异的两点,证明:直线PQ的斜率大于0;
(2)求实数a的取值范围,使不等式f(x)≥axcosx在 上恒成立.
上恒成立.
解:(1)∵f(x)=x+sinx
∴f'(x)=1+cosx≥0
∴函数f(x)在R上单调递增
设P(x1,y1),Q(x2,y2)则 ,即kPQ>0
,即kPQ>0
∴直线PQ的斜率大于0;
(2)依题意得,设 ,
,
1°当a≤0时,Q(x)≤0恒成立; …(8分)
2°当a>0时,Q'(x)=(a-1)cosx-axsinx-1,…(10分)
①0<a≤2时,Q'(x)≤0,Q(x)在 上单调递减,
上单调递减,
所以Q(x)≤Q(0)=0恒成立;…(12分)
②a>2时,注意到当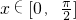 时,x≥sinx,
时,x≥sinx,
于是Q(x)=axcosx-x-sinx≥axcosx-2x=x(acosx-2),
必存在 ,使得当x∈(0,x0)时,有Q(x0)>0,不能使Q(x)≤0恒成立.
,使得当x∈(0,x0)时,有Q(x0)>0,不能使Q(x)≤0恒成立.
综上所述,实数a的取值范围为a≤2. …(16分)
分析:(1)先利用导数研究函数的单调性,然后设P(x1,y1),Q(x2,y2),根据斜率的定义建立关系式,从而可知可证结论;
(2)设 ,然后利用导数研究函数的最小值,使得Q(x)min≥0即可.
,然后利用导数研究函数的最小值,使得Q(x)min≥0即可.
点评:本题主要考查函数的概念、性质及导数等基础知识,考查灵活运用数学结合、分类讨论的思想进行探究、分析与解决问题的能力.
∴f'(x)=1+cosx≥0
∴函数f(x)在R上单调递增
设P(x1,y1),Q(x2,y2)则
 ,即kPQ>0
,即kPQ>0∴直线PQ的斜率大于0;
(2)依题意得,设
 ,
,1°当a≤0时,Q(x)≤0恒成立; …(8分)
2°当a>0时,Q'(x)=(a-1)cosx-axsinx-1,…(10分)
①0<a≤2时,Q'(x)≤0,Q(x)在
 上单调递减,
上单调递减,所以Q(x)≤Q(0)=0恒成立;…(12分)
②a>2时,注意到当
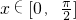 时,x≥sinx,
时,x≥sinx,于是Q(x)=axcosx-x-sinx≥axcosx-2x=x(acosx-2),
必存在
 ,使得当x∈(0,x0)时,有Q(x0)>0,不能使Q(x)≤0恒成立.
,使得当x∈(0,x0)时,有Q(x0)>0,不能使Q(x)≤0恒成立.综上所述,实数a的取值范围为a≤2. …(16分)
分析:(1)先利用导数研究函数的单调性,然后设P(x1,y1),Q(x2,y2),根据斜率的定义建立关系式,从而可知可证结论;
(2)设
 ,然后利用导数研究函数的最小值,使得Q(x)min≥0即可.
,然后利用导数研究函数的最小值,使得Q(x)min≥0即可.点评:本题主要考查函数的概念、性质及导数等基础知识,考查灵活运用数学结合、分类讨论的思想进行探究、分析与解决问题的能力.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|