题目内容
本大题满分13分)
已知函数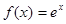 ,过该函数图象上点
,过该函数图象上点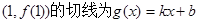
(Ⅰ)证明: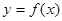 图象上的点总在
图象上的点总在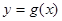 图象的上方;
图象的上方;
(Ⅱ)若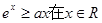 上恒成立,求实数
上恒成立,求实数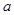 的取值范围.
的取值范围.
【答案】
解:(Ⅰ) ,
,
设
 为增,
为增,
当
 ,
,
所以 图象上的点总在
图象上的点总在 图象的上方. …………………………6分
图象的上方. …………………………6分
(Ⅱ)当 .
.
|
x |
(-∞,0) |
(0,1) |
1 |
(1,+∞) |
|
F‘(x) |
- |
- |
0 |
+ |
|
F(x) |
减 |
减 |
e |
增 |
①当x>0时,F(x)在x=1时有最小值e, .
.
②当x<0时,F(x)为减函数,
 ,
,
 .
.
③当x=0时, ∈R.
∈R.
由①②③, 恒成立的
恒成立的 的范围是
的范围是 .
………………13分
.
………………13分
【解析】略

练习册系列答案
相关题目
 (1)当圆柱底面半径
(1)当圆柱底面半径 ,设
,设 ,数列
,数列 .
.  是等差数列;
是等差数列; 的前n项和Sn;
的前n项和Sn; 一切正整数n恒成立,求实数m的取值范围.
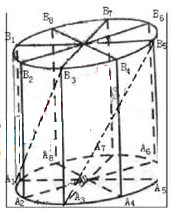
一切正整数n恒成立,求实数m的取值范围. 的扇形铁皮
的扇形铁皮 ,欲从其中裁剪出一块内接五边形
,欲从其中裁剪出一块内接五边形 ,使点
,使点 在
在 弧上,点
弧上,点 分别在半径
分别在半径 和
和 上,四边形
上,四边形 是矩形,点
是矩形,点 在弧
在弧 上,
上, 点在线段
点在线段 上,四边形
上,四边形 是直角梯形.现有如下裁剪方案:先使矩形
是直角梯形.现有如下裁剪方案:先使矩形 ,当矩形
,当矩形 的值;
的值;
 是椭圆
是椭圆 右焦点,点
右焦点,点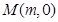 、
、 分别是x轴、 y上的动点,且满足
分别是x轴、 y上的动点,且满足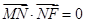 ,若点
,若点 满足
满足 .
. 的方程;
的方程; 、
、 两点,直线
两点,直线 、
、 与直线
与直线 分别交于点
分别交于点 、
、 (其中
(其中 为坐标原点),试判断
为坐标原点),试判断 是否为定值?若是,求出这个定值;若不是,请说明理由.
是否为定值?若是,求出这个定值;若不是,请说明理由. 是定义域在
是定义域在 上的单调函数,且对于任意正数
上的单调函数,且对于任意正数 有
有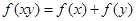 ,已知
,已知 .
.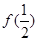 的值;
的值; 满足:
满足: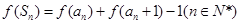 ,其中
,其中 是数列
是数列 ,使
,使

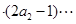
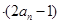 对一切
对一切 成立?若存在,求出M的取值范围;若不存在,说明理由.
成立?若存在,求出M的取值范围;若不存在,说明理由.