题目内容
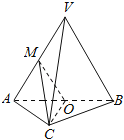
【题目】如图,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .直角梯形
.直角梯形![]() 通过直角梯形
通过直角梯形![]() 以直线
以直线![]() 为轴旋转得到,且使平面
为轴旋转得到,且使平面![]() 平面
平面![]() .
. ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的动点.
上的动点.

(1)求证: ![]() ;
;
(2)当点![]() 是线段
是线段![]() 中点时,求二面角
中点时,求二面角![]() 的余弦值;
的余弦值;
(3)是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?请说明理由.
?请说明理由.
【答案】(1)见解析(2) ![]() (3)存在点
(3)存在点![]() ,使得直线
,使得直线![]() 平面
平面![]()
【解析】试题分析:(Ⅰ)由![]() 平面
平面![]() 平面
平面![]() ..推出
..推出![]() 平面
平面![]() .即可证明
.即可证明![]() .
.
(Ⅱ)以AC,AB,AA1为x轴、y轴、z轴建立空间直角坐标系,求出平面ABM的一个法向量,平面APM的一个法向量,利用空间向量的数量积求解二面角P﹣AM﹣B的余弦值.
(Ⅲ)存在点P,使得直线A1C∥平面AMP.设P(x1,y1,z1),求出平面AMP的一个法向量,求出![]() ,利用
,利用![]() .求出λ,即可证明结果.
.求出λ,即可证明结果.
试题解析:
(1)由已知![]() ,平面
,平面![]() 平面
平面![]()
![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() 平面
平面![]()
所以![]()
(2)由(1)可知![]() ,
, ![]() ,
, ![]() 两两垂直.
两两垂直.
分别以![]() ,
, ![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系如图所示.
轴建立空间直角坐标系如图所示.
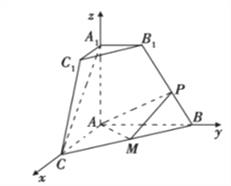
由已知![]()
![]()
所以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
因为![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 的中点.
的中点.
所以![]() ,
, ![]()
易知平面![]() 的一个法向量
的一个法向量![]()
设平面![]() 的一个法向量为
的一个法向量为![]()
由![]() 得
得
取![]() ,得
,得![]()
由图可知,二面角![]() 的大小为锐角,
的大小为锐角,
所以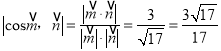
所以二面角![]() 的余弦值为
的余弦值为![]()
(3)存在点![]() ,使得直线
,使得直线![]() 平面
平面![]()
设![]() ,且
,且![]() ,
, ![]() ,则
,则![]()
所以![]() ,
, ![]() ,
, ![]() .所以
.所以![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由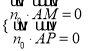 得
得![]()
取![]() ,得
,得![]() (
(![]() 不符合题意)
不符合题意)
又![]() 若
若![]() 平面
平面![]() ,则
,则![]()
所以![]() ,所以
,所以![]()
所以存在点![]() ,使得直线
,使得直线![]() 平面
平面![]()

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目