题目内容
设(1)求函数![]() 的单调递增,递减区间;
的单调递增,递减区间;
(2)当x∈[-1,2]时,![]() <m恒成立,求实数m的取值范围.
<m恒成立,求实数m的取值范围.
解:(1) ![]() =3x2-x-2,令
=3x2-x-2,令![]() =0,
=0,
即3x2-x-2=0![]() x=1或x=
x=1或x=![]() .
.
所以当x∈(-∞,![]() )时,
)时,![]() >0,
>0, ![]() 为增函数;
为增函数;
当x∈(![]() ,1)时,
,1)时,![]() <0,
<0, ![]() 为减函数;
为减函数;
当x∈(1,+∞)时, ![]() >0,
>0, ![]() 为增函数.
为增函数.
所以![]() 的递增区间为(-∞,
的递增区间为(-∞,![]() )和(1, +∞),
)和(1, +∞), ![]() 的递减区间为(
的递减区间为(![]() ,1).
,1).
(2)当x∈[-1,2]时, ![]() <m恒成立,只需使
<m恒成立,只需使![]() 在[-1,2]上的最大值小于m即可.
在[-1,2]上的最大值小于m即可.
由(1)知![]() =
=![]() =5+
=5+![]() ,
,![]() =
=![]() =
=![]() .又
.又![]() =
=![]() ,
,![]() =7,所以
=7,所以![]() 在[-1,2]上的最大值为
在[-1,2]上的最大值为![]() =7.所以m>7.
=7.所以m>7.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 -2x+5
-2x+5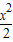 -2x+5
-2x+5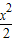 -2x+5
-2x+5