题目内容
设f(x)=x3-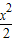 -2x+5
-2x+5(1)求函数f(x)的极值;
(2)当x∈[-1,2]时,f(x)<m恒成立,求实数m的取值范围..
【答案】分析:(1)先利用导数求函数f(x)=x3-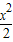 -2x+5的单调区间,从而确定函数的极值;
-2x+5的单调区间,从而确定函数的极值;
(2)恒成立问题可转化成f(x)max<m即可.函数在[-1,2]上的最大值,利用极值与端点的函数值可以确定.
解答:解:(1)f′(x)=3x2-x-2=0,解得x=1,- ,
,
∵函数在(-∞,- ),(1,+∞)上单调增,在(-
),(1,+∞)上单调增,在(- ,1)上单调减
,1)上单调减
∴函数的极大值为f(- )=5
)=5 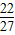 ,极小值f(1)=3
,极小值f(1)=3  ,
,
(2)∵f(-1)=5 ,f(-
,f(- )=5
)=5 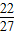 ,f(1)=3
,f(1)=3  ,f(2)=7;
,f(2)=7;
即f(x)max=7,
要使当x∈[-1,2]时,f(x)<m恒成立,只需f(x)max<m即可
故实数m的取值范围为(7,+∞)
点评:本题以函数为载体,考查函数的单调性,考查函数的极值,同时考查了恒成立问题的处理,注意利用好导数工具.
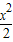 -2x+5的单调区间,从而确定函数的极值;
-2x+5的单调区间,从而确定函数的极值;(2)恒成立问题可转化成f(x)max<m即可.函数在[-1,2]上的最大值,利用极值与端点的函数值可以确定.
解答:解:(1)f′(x)=3x2-x-2=0,解得x=1,-
 ,
,∵函数在(-∞,-
 ),(1,+∞)上单调增,在(-
),(1,+∞)上单调增,在(- ,1)上单调减
,1)上单调减∴函数的极大值为f(-
 )=5
)=5 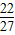 ,极小值f(1)=3
,极小值f(1)=3  ,
,(2)∵f(-1)=5
 ,f(-
,f(- )=5
)=5 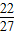 ,f(1)=3
,f(1)=3  ,f(2)=7;
,f(2)=7;即f(x)max=7,
要使当x∈[-1,2]时,f(x)<m恒成立,只需f(x)max<m即可
故实数m的取值范围为(7,+∞)
点评:本题以函数为载体,考查函数的单调性,考查函数的极值,同时考查了恒成立问题的处理,注意利用好导数工具.

练习册系列答案
相关题目
设f(x)=x3+bx+c是[-1,1]上的增函数,且f(-
)•f(
)<0,则方程f(x)=0在[-1,1]内( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、可能有3个实数根 |
| B、可能有2个实数根 |
| C、有唯一的实数根 |
| D、没有实数根 |