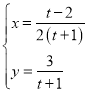题目内容
【题目】已知直线l： 
椭圆C： 
，
分别为椭圆的左右焦点.
（1）当直线l过右焦点
时，求C的标准方程；
（2）设直线l与椭圆C交于A，B两点，O为坐标原点，若∠AOB是钝角，求实数a的取值范围.
【答案】（1）
（2）
.
【解析】
（1）将右焦点代入直线方程，结合椭圆中的
及
关系，即可求得
，进而得椭圆方程.
（2）设
，联立直线与椭圆方程，化简后由判别式可确定a的范围；并由韦达定理表示出
、
，进而表示出
，由
为钝角并结合平面向量数量积的坐标运算，即可求得a的取值范围.
（1）直线l过右焦点
，则
，代入直线方程可得
，
椭圆C： 
，
所以
解得
所以椭圆C的方程为，
（2）由题可得，设，
则
化简可得得
，
由
，因
即
①
由韦达定理得，
，
，
因为
，
因为钝角，所以
，
即
所以 
，
即
所以
， ②
综上所述，由①②得
的取值范围为.
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
