题目内容
已知函数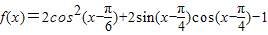 .
.(1)求函数f(x)的最小正周期和图象的对称轴方程;
(2)求函数f(x)在区间
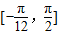 上的值域.
上的值域.
【答案】分析:(1)通过二倍角公式与两角和的正弦函数化简函数的表达式,化简为一个角的一个三角函数的形式,利用周期公式求函数f(x)的最小正周期,利用正弦函数的对称轴方程求出函数的图象的对称轴方程;
(2)通过x∈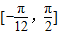 ,求出
,求出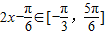 ,利用函数的单调性求出函数在
,利用函数的单调性求出函数在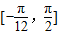 上的值域,即可.
上的值域,即可.
解答:解:(1)∵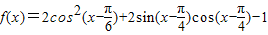
=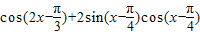
=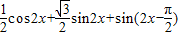
=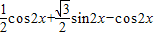
=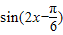 …(5分)
…(5分)
∴周期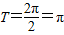 .由
.由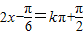 ,得
,得 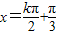 (k∈Z)
(k∈Z)
∴函数图象的对称轴方程为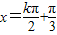 (k∈Z)…(7分)
(k∈Z)…(7分)
(2)∵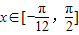 ,∴
,∴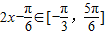 ,
,
又∵f(x)=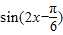 在区间
在区间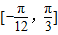 上单调递增,
上单调递增,
在区间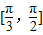 上单调递减,∴当
上单调递减,∴当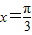 时,f(x)取最大值1.
时,f(x)取最大值1.
又∵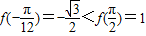 ,∴当
,∴当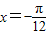 时,f(x)取最小值
时,f(x)取最小值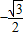 .
.
∴函数f(x)在区间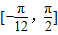 上的值域为
上的值域为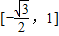 .…(12分)
.…(12分)
点评:本题是中档题,考查三角函数的化简求值,函数的周期的求法,以及函数的闭区间上的最值的应用,考查计算能力,高考常考题型.
(2)通过x∈
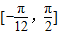 ,求出
,求出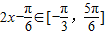 ,利用函数的单调性求出函数在
,利用函数的单调性求出函数在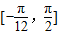 上的值域,即可.
上的值域,即可.解答:解:(1)∵
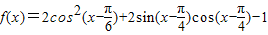
=
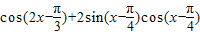
=
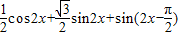
=
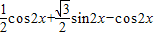
=
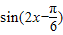 …(5分)
…(5分)∴周期
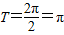 .由
.由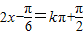 ,得
,得 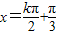 (k∈Z)
(k∈Z)∴函数图象的对称轴方程为
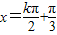 (k∈Z)…(7分)
(k∈Z)…(7分)(2)∵
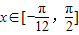 ,∴
,∴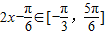 ,
,又∵f(x)=
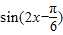 在区间
在区间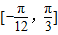 上单调递增,
上单调递增,在区间
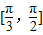 上单调递减,∴当
上单调递减,∴当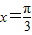 时,f(x)取最大值1.
时,f(x)取最大值1.又∵
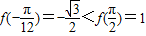 ,∴当
,∴当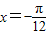 时,f(x)取最小值
时,f(x)取最小值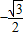 .
.∴函数f(x)在区间
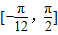 上的值域为
上的值域为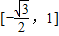 .…(12分)
.…(12分)点评:本题是中档题,考查三角函数的化简求值,函数的周期的求法,以及函数的闭区间上的最值的应用,考查计算能力,高考常考题型.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.