题目内容
已知随机变量ξ的分布列为ξ | -2 | -1 | 0 | 1 | 2 | 3 |
P |
|
|
|
|
|
|
分别求出随机变量η1=
ξ,η2=ξ2的分布列.
解：由于η1=
ξ对于不同的ξ有不同的取值满足y=
x，即y1=
x1=-1,
y2=
x2=
,y3=
x3=0,y4=x4=
,y5=
x5=1,y6=
x6=
，所以η1的分布列为
η1 | -1 |
| 0 |
| 1 |
|
P |
|
|
|
|
|
|
η2=ξ2对于ξ的不同取值-2，2及-1，1，η2分别取相同的值4与1，即η2取4这个值的概率应是ξ取-2与2值的概率
合并的结果，η2取1这个值的概率就是ξ取-1与1值的概率
合并的结果，故η2的分布列为
η2 | 0 | 1 | 4 | 9 |
P |
|
|
|
|
练习册系列答案
相关题目
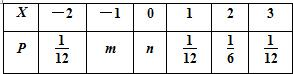已知随机变量X的分布列如图：其中m，n∈[0，1），且E（X）=| 1 |
| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|