题目内容
点集{(x,y)|||x|-1|+|y|=2}的图形是一条封闭的折线,这条封闭折线所围成的区域的面积是( )
分析:分析方程的特征可得,方程的曲线关于x轴、y轴、及原点对称,画出曲线在第一象限内的情况,求出曲线在第一象限内围成的图形的面积,乘以4,即得所求.
解答:解:由于方程|||x|-1|+|y|=2 中,把x换成-x,方程不变,故方程表示的曲线关于y轴对称;
把y换成-y,方程也不变,故方程表示的曲线关于x轴及原点都对称,
即点集{(x,y)|||x|-1|+|y|=2}的图形关于x轴、y轴、及原点对称.
先考虑曲线位于第一象限及坐标轴上的情况.
令x≥0,y≥0,方程化为 y=2-|x|,表示线段AB 和BC,如图所示:
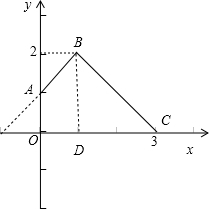
曲线在第一象限内围成的图形的面积等于直角梯形OABD的面积,加上直角三角形BDC的面积.
而直角梯形OABD的面积为
=
,直角三角形BDC的面积等于
×2×2=2,
故曲线在第一象限内围成的图形的面积等于
+2=
,
故整条封闭折线所围成的区域的面积是4×
=14,
故选A.
把y换成-y,方程也不变,故方程表示的曲线关于x轴及原点都对称,
即点集{(x,y)|||x|-1|+|y|=2}的图形关于x轴、y轴、及原点对称.
先考虑曲线位于第一象限及坐标轴上的情况.
令x≥0,y≥0,方程化为 y=2-|x|,表示线段AB 和BC,如图所示:

曲线在第一象限内围成的图形的面积等于直角梯形OABD的面积,加上直角三角形BDC的面积.
而直角梯形OABD的面积为
| (1+2)×1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
故曲线在第一象限内围成的图形的面积等于
| 3 |
| 2 |
| 7 |
| 2 |
故整条封闭折线所围成的区域的面积是4×
| 7 |
| 2 |
故选A.
点评:本题主要考查带有绝对值的函数的图象特征,函数的对称性的应用,体现了分类讨论与数形结合的数学思想,属于中档题.

练习册系列答案
相关题目