题目内容
已知两点A（1，0），B（1，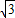
），O为坐标原点，点C在第二象限，且∠AOC=120°，设
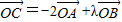，（λ∈R），则λ等于（ ）A．-1
B．1
C．-2
D．2
【答案】分析：先设点C的坐标，根据题意和向量的坐标运算，分别用λ表示x和y，再由向量的数量积的坐标表示出∠AOC的余弦值，再求出λ的值．
解答：解：设点C的坐标是（x，y），则由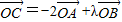
得，
（x，y）=-2（1，0）+λ（1，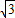
）=（-2+λ，
），
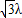∴x=-2+λ，y=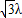
，
又∵∠AOC=120°，∴cos120°=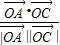
，即-
=
，
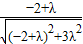解得，λ=1．
故选B．
点评：本题考查向量的数量积和向量的坐标运算的应用，即通过条件列出关系式，利用向量相等的坐标等价条件进行求值．
解答：解：设点C的坐标是（x，y），则由
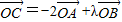得，（x，y）=-2（1，0）+λ（1，
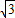）=（-2+λ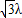，），∴x=-2+λ，y=
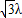，又∵∠AOC=120°，∴cos120°=
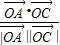，即-=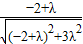，解得，λ=1．
故选B．
点评：本题考查向量的数量积和向量的坐标运算的应用，即通过条件列出关系式，利用向量相等的坐标等价条件进行求值．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
已知两点A（-1，0），B（0，2），点P是圆（x-1）2+y2=1上任意一点，则△PAB面积的最大值与最小值分别是（ ）
A、2，
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|