Question

【题目】已知a，b分别是△ABC内角A，B的对边，且bsin2A＝acos Asin B，函数f(x)＝sin Acos2x－sin2sin 2x，x∈.

(1)求A；

(2)求函数f(x)的值域.

Answer 1

【答案】(1) ；(2) .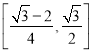

【解析】试题分析：

（1）由已知结合正弦定理，求出的值，从而求出的值；

（2）由化简函数为正弦型函数，求出时的值域即可.

试题解析：

(1)在△ABC中，bsin2A＝acos Asin B，

由正弦定理得，sin Bsin2A＝sin Acos Asin B，

又A，B为△ABC的内角，故sin Asin B≠0，

∴tan A＝＝，

又A∈(0，π)，∴A＝.

(2)由A＝，

∴函数f(x)＝sin Acos2x－sin2sin 2x

＝cos2x－sin 2x

＝·－·sin 2x

＝－＋

＝－sin＋，

∵x∈，∴－≤2x－≤，

∴－≤sin≤1，

∴≤－sin＋≤，

所以f(x)的值域为.