题目内容
在△ABC中，∠ACB=90°，CD⊥AB于D，E为AC的中点，DE的延长线交BC的延长线于F.
求证：△BDF∽△DCF.
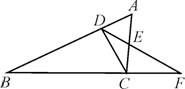
证明：∵E为AC中点，∴DE=CE.
∴∠CDF=∠ACD.
又∠ACB=90°，CD⊥AB，
∴∠ACD=∠B.
∴∠CDF=∠B.
又∠F为公共角，
∴△BDF∽△DCF.
练习册系列答案
相关题目
题目内容
在△ABC中，∠ACB=90°，CD⊥AB于D，E为AC的中点，DE的延长线交BC的延长线于F.
求证：△BDF∽△DCF.
证明：∵E为AC中点，∴DE=CE.
∴∠CDF=∠ACD.
又∠ACB=90°，CD⊥AB，
∴∠ACD=∠B.
∴∠CDF=∠B.
又∠F为公共角，
∴△BDF∽△DCF.
如图，在△ABC中，AC=2，BC=1，
如图，在△ABC中，AC=BC，AB=2，O为AB的中点，沿OC将△AOC折起到△A′OC的位置，使得直线A′B与平面ABC成30°角．