题目内容
设［a,b］是函数y=f(x)定义域内的一个闭区间.如果对任意的x1、x2∈［a,b］且x1≠x2,有f(
)＞
［f(x1)+f(x2)］,那么称函数y=f(x)在区间［a,b］上为凸函数;如果对任意的x1、x2∈［a,b］,且x1≠x2,有f(
)＜
［f(x1)+f(x2)］,那么称函数y=f(x)在区间［a,b］上为凹函数.(1)判定函数f(x)=x在定义域［0,+∞)上是凹函数还是凸函数,并证明你的结论.
(2)判定函数f(x)=2x在定义域(-∞,+∞)上是凹函数还是凸函数,并证明之.
解:(1)函数y=x的图象如下:
由图形易知,任给x1、x2∈［0,+∞),
＞(
),
∴函数f(x)=
在［0,+∞)上为凸函数.
证明:任取x1、x2∈［0,+∞),且x1≠x2,
(
)2-［
(
)］2
=
(x1+x2-2
)=
(
)2＞0,
∴(
)2＞［
(
)］2.
∴
＞
(
),
即满足f(
)＞
［f(x1)+f(x2)］.
∴函数f(x)=x在［0,+∞)上是凸函数.
(2)函数f(x)=2x图象如下.
从图形知在(-∞,+∞)上函数y=2x是凹函数.
证明:任取x1、x2∈(-∞,+∞)且x1≠x2,
则2
-
(
)=-
(
-2
)=-
(
)2.
∵x1≠x2,∴
≠
,即
.
∴-
(
)2＜0,即2
＜
(
).
∴函数f(x)=2x在(-∞,+∞)上是凹函数.
练习册系列答案
相关题目
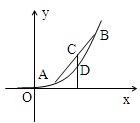设a，b，λ都为正数，且a≠b，对于函数y=x2（x＞0）图象上两点A（a，a2），B（b，b2）．
)＞
［f(x1)+f(x2)］,那么称函数y=f(x)在区间［a,b］上为凸函数;如果对任意的x1、x2∈［a,b］,且x1≠x2,有f(
)＜
［f(x1)+f(x2)］,那么称函数y=f(x)在区间［a,b］上为凹函数.
在定义域［0,+∞)上是凹函数还是凸函数,并证明你的结论;
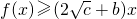对任意x∈R+恒成立”的既不充分也不必要条件