题目内容
在半径为R的球内放入大小相等的4个小球,则小球半径r的最大值为( )
分析:由题意,四个小球两两相切并且四个小球都与大球相切时,这些小球的半径最大,以四个小球球心为顶点的正四面体棱长为2r,该正四面体的中心(外接球球心)就是大球的球心,求出正四面体的外接球半径,即可求得结论.
解答:解:由题意,四个小球两两相切并且四个小球都与大球相切时,这些小球的半径最大.
以四个小球球心为顶点的正四面体棱长为2r,该正四面体的中心(外接球球心)就是大球的球心
该正四面体的高为
=
设正四面体的外接球半径为x,则x2=(
-x)2+(
)2
∴x=
r
∴R=
r+r,
∴r=(
-2)R.
故选A.
以四个小球球心为顶点的正四面体棱长为2r,该正四面体的中心(外接球球心)就是大球的球心
该正四面体的高为
4r2-(
|
2
| ||
| 3 |
设正四面体的外接球半径为x,则x2=(
2
| ||
| 3 |
2
| ||
| 3 |
∴x=
| ||
| 2 |
∴R=
| ||
| 2 |
∴r=(
| 6 |
故选A.
点评:本题考查点、线、面距离的计算,考查学生分析解决问题的能力,确定四个小球两两相切并且四个小球都与大球相切时,这些小球的半径最大是关键.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
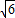 -2)R
-2)R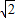 -1)R
-1)R R
R R
R -2)R
-2)R -1)R
-1)R R
R R
R