题目内容
已知函数 .
.
(Ⅰ)求 的最小正周期和对称中心;
的最小正周期和对称中心;
(Ⅱ)若将 的图像向左平移
的图像向左平移 个单位后所得到的图像关于
个单位后所得到的图像关于 轴对称,求实数
轴对称,求实数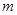 的最小值.
的最小值.
 .
.(Ⅰ)求
 的最小正周期和对称中心;
的最小正周期和对称中心;(Ⅱ)若将
 的图像向左平移
的图像向左平移 个单位后所得到的图像关于
个单位后所得到的图像关于 轴对称,求实数
轴对称,求实数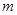 的最小值.
的最小值.(Ⅰ) ,
, ; (Ⅱ)
; (Ⅱ) .
.
 ,
, ; (Ⅱ)
; (Ⅱ) .
.试题分析:(Ⅰ)这一问关键是利用倍角公式化简表达式;(Ⅱ)先利用平移得到表达式,再根据图像关于
 轴对称得到
轴对称得到 ,解出
,解出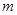 .
.试题解析:(Ⅰ)



 3分
3分由
 得,
得,
所以最小正周期是
 ,对称中心为
,对称中心为 ,
, . 6分
. 6分(Ⅱ)将
 的图像向左平移
的图像向左平移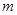 个单位后得到,
个单位后得到, 8分
8分所以
 ,
, .因为
.因为 ,所以
,所以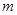 的最小值为
的最小值为 . 12分
. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 和
和 ,
, ,写出函数
,写出函数 的最小正周期;并求函数
的最小正周期;并求函数 的单调区间;
的单调区间;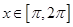 ,求
,求 的最大值.
的最大值. ,
,
 的值;
的值;  ,且
,且 ,求
,求 .
. 函数
函数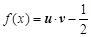 的最小正周期为
的最小正周期为 .
. 的值;
的值; 在区间
在区间 上的值域.
上的值域. ,
, .
. 的最小值和最小正周期;
的最小值和最小正周期; 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
,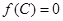 且
且 ,求
,求
 ,
, ,
, 在
在 上的部分图象如图所示,则
上的部分图象如图所示,则 的值为 .
的值为 .
 .
.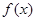 的最小值,并求使
的最小值,并求使 的集合;
的集合; 的图像可由
的图像可由 的图象经过怎样的变化得到.
的图象经过怎样的变化得到. 的结果是( )
的结果是( )


