题目内容
有下列五个命题:
①平面内,到一定点的距离等于到一定直线距离的点的集合是抛物线;
②在平面内,F1、F2是定点, ,动点M满足
,动点M满足 ,则点M的轨迹是椭圆;
,则点M的轨迹是椭圆;
③“在 中,“
中,“ ”是“
”是“ 三个角成等差数列”的充要条件;
三个角成等差数列”的充要条件;
④“若 则方程
则方程 是椭圆”。
是椭圆”。
⑤已知向量 是空间的一个基底,则向量
是空间的一个基底,则向量 也是空间的一个基底。其中真命题的序号是 .
也是空间的一个基底。其中真命题的序号是 .
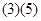
解析① 平面内,到一定点的距离等于到一定直线距离的点的集合是抛物线;要求定点不在定直线上,否则点的轨迹为过定点且垂直于定直线的一条直线
② 椭圆定义为到两定点的距离之和为定值的点的集合,这里要求这个和值要大于两定点间的距离,等于两定点间的距离的轨迹为两定点连线段。
③  三个角成等差数列可以推到
三个角成等差数列可以推到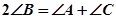 ,又因为
,又因为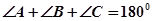 ,所以
,所以 ,而由
,而由 ,
,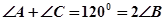 即
即 三个角成等差数列,所以“
三个角成等差数列,所以“ ”是“
”是“ 三个角成等差数列”的充要条件;
三个角成等差数列”的充要条件;
④ 当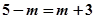 时,即
时,即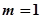 时,该方程表示圆
时,该方程表示圆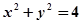
⑤ 假设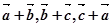 共面,则存在实数λ、μ,使得
共面,则存在实数λ、μ,使得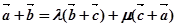
∴
∵{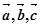 }为基底
}为基底
∴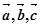 不共面
不共面
∴1=μ,1=λ,0=λ+μ
此方程组无解
∴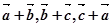 不共面
不共面

练习册系列答案
相关题目
 ,动点M满足
,动点M满足 ,则点M的轨迹是椭圆;
,则点M的轨迹是椭圆; 中,“
中,“ ”是“
”是“ 三个角成等差数列”的充要条件;
三个角成等差数列”的充要条件; 则方程
则方程 是椭圆”。
是椭圆”。 是空间的一个基底,则向量
是空间的一个基底,则向量 也是空间的一个基底。其中真命题的序号是
.
也是空间的一个基底。其中真命题的序号是
.