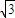题目内容
我们把双曲线中半焦距与半实轴的比值,即
称为双曲线的离心率.已知过双曲线
-
=1(a>0,b>0)左焦点F1作x轴的垂线交双曲线于点P,F2为右焦点,若∠F1PF2=60°,则该双曲线的离心率为( )
| c |
| a |
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
分析:根据题意可知∠F1PF2=60°,在Rt△F1PF2中求得2|F1P|=|PF2|,2C=
|F1P|,进而根据双曲线的定义求得|F1P|=2a,代入离心率公式中求得答案.
| 3 |
解答:解:依题意可知∠F1PF2=60°
∴2|F1P|=|PF2|,|F1F2|=2C=
|F1P|
∵根据双曲线的定义可知|PF2|-|F1P|=|F1P|=2a
∴a=
|F1P|
∴
=
=
=
故选C
∴2|F1P|=|PF2|,|F1F2|=2C=
| 3 |
∵根据双曲线的定义可知|PF2|-|F1P|=|F1P|=2a
∴a=
| 1 |
| 2 |
∴
| c |
| a |
| ||||
|
| ||||
|
| 3 |
故选C
点评:本题主要考查了双曲线的简单性质.考查了双曲线标准方程中a,b和c的关系的应用.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 称为双曲线的离心率.已知过双曲线
称为双曲线的离心率.已知过双曲线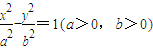 左焦点F1作x轴的垂线交双曲线于点P,F2为右焦点,若∠F1PF2=60°,则该双曲线的离心率为( )
左焦点F1作x轴的垂线交双曲线于点P,F2为右焦点,若∠F1PF2=60°,则该双曲线的离心率为( )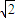
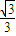
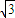
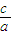 称为双曲线的离心率.已知过双曲线
称为双曲线的离心率.已知过双曲线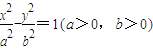 左焦点F1作x轴的垂线交双曲线于点P,F2为右焦点,若∠F1PF2=60°,则该双曲线的离心率为( )
左焦点F1作x轴的垂线交双曲线于点P,F2为右焦点,若∠F1PF2=60°,则该双曲线的离心率为( )