题目内容
已知椭圆的短轴长为2a,焦点是F1(-(1)求椭圆的方程;
(2)求直线l的方程.
解析:(1)∵F1到直线x=-![]() 的距离为
的距离为![]() ,?
,?
∴-![]() +
+![]() =
=![]() .
.
∴a2=4.
而c=3,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,
∴所求椭圆的方程为![]() +y2=1.?
+y2=1.?
(2)设A(x1,y1)、B(x2,y2).?
∵|F2B|=3|F2A|,?
∴

∵A、B在椭圆![]() +y2=1上,
+y2=1上,
∴
解得
∴l的斜率为
∴l的方程为y=![]() (x-
(x-![]() ),
),
即![]() x-y-
x-y-![]() =0.
=0.

练习册系列答案
相关题目
 已知椭圆的短轴长为2
已知椭圆的短轴长为2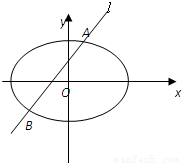 已知椭圆的短轴长为2
已知椭圆的短轴长为2 ,焦点坐标分别是(-1,0)和(1,0).
,焦点坐标分别是(-1,0)和(1,0). ,焦点坐标分别是(-1,0)和(1,0),
,焦点坐标分别是(-1,0)和(1,0), 的短轴长为2,且与抛物线
的短轴长为2,且与抛物线 有共同的焦点,椭圆C的左顶点为A,右顶点为B,点P是椭圆C上位于x轴上方的动点,直线AP,BP与直线y=3分别交于G,H两点.
有共同的焦点,椭圆C的左顶点为A,右顶点为B,点P是椭圆C上位于x轴上方的动点,直线AP,BP与直线y=3分别交于G,H两点.