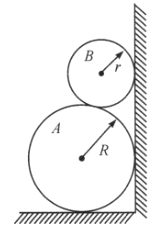
题目内容
【题目】长为![]() 的均匀细杆,一端放在水平地面上,同时斜搁在半径为
的均匀细杆,一端放在水平地面上,同时斜搁在半径为![]() 的匀质圆柱上,如图所示,三个接触处的摩擦因数均为
的匀质圆柱上,如图所示,三个接触处的摩擦因数均为![]() .证明:
.证明:
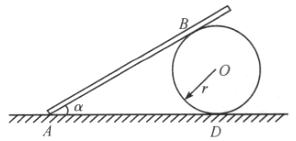
(1)如果![]() ,则平衡时杆与地面间的最大倾角
,则平衡时杆与地面间的最大倾角![]() .
.
(2)如果![]() ,则当平衡时,最大倾角由下列方程确定:
,则当平衡时,最大倾角由下列方程确定: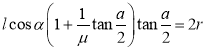 .
.
【答案】证明见解析
【解析】
(i)由圆柱体的平衡条件可知,![]() 两处的摩擦力总是一样大的,如果要在
两处的摩擦力总是一样大的,如果要在![]() 两处产生滑动,则一定是
两处产生滑动,则一定是![]() 处先滑动;(i)由平衡时三力共点的条件可知,杆对圆柱体在
处先滑动;(i)由平衡时三力共点的条件可知,杆对圆柱体在![]() 点的作用力(约束反力)一定过
点的作用力(约束反力)一定过![]() 点。
点。
由此可知,圆柱体对杆的作用力方向总是沿![]() 方向的,不论其是否处于临界状态。
方向的,不论其是否处于临界状态。
我们首先讨论杆的平衡条件:
由于杆与外界有![]() 两处接触,哪一处先达到临界状态都是有可能的,因此,在一系列的可能状态中,我们挑选一特定状态,即
两处接触,哪一处先达到临界状态都是有可能的,因此,在一系列的可能状态中,我们挑选一特定状态,即![]() 同时达到临界状态时,杆长
同时达到临界状态时,杆长![]() 与圆柱半径应满足的关系,此刻的
与圆柱半径应满足的关系,此刻的![]() 用
用![]() 表示.
表示.

由图乙中几何关系易知,杆的上端应在过![]() 点的竖直线上,则
点的竖直线上,则
 ,
,
其中![]() ,
,
且![]() .
.
所以, .
.
(1)![]() 时,讨论其平衡。
时,讨论其平衡。
当![]() 时,杆的质心
时,杆的质心![]() 将沿杆下移,图乙中
将沿杆下移,图乙中![]() 点上移到
点上移到![]() 点(
点(![]() 点仍保持临界),此时
点仍保持临界),此时![]() 点受力通过
点受力通过![]() 点,系统才能保持平衡,
点,系统才能保持平衡,![]() 点处的作用力方向变为
点处的作用力方向变为![]() 方向,与法向的交角小于
方向,与法向的交角小于![]() .在这种情况下,即
.在这种情况下,即![]() 处处于临界,
处处于临界,![]() 处未达到临界,这种情况仍然属于系统(杆)处于临界状态,而杆与地面的交角
处未达到临界,这种情况仍然属于系统(杆)处于临界状态,而杆与地面的交角![]() 仍然是杆达到临界平衡时的最大交角.
仍然是杆达到临界平衡时的最大交角.
显然,在这种情况下,还有一几何约束,即![]() 不能小于
不能小于![]() ,即不能小于
,即不能小于![]() ,否则杆就不能搁在圆柱上了.考虑到
,否则杆就不能搁在圆柱上了.考虑到 ,所以,条件统一表示为
,所以,条件统一表示为
 ,或
,或![]() .
.
在此情况下,杆与地面间的夹角![]() 满足
满足
![]() ,即
,即![]() .
.
(2)![]() 时,讨论其平衡。
时,讨论其平衡。
在![]() 不变的情况下,当
不变的情况下,当![]() 时,
时,![]() 点将沿杆上移,此时通过
点将沿杆上移,此时通过![]() 点的竖直线与圆柱对杆的作用方向上的直线交于
点的竖直线与圆柱对杆的作用方向上的直线交于![]() ,
,![]() 在
在![]() 点之下.如果系统还要达到平衡,三力必须交于
点之下.如果系统还要达到平衡,三力必须交于![]() ,但是,此时
,但是,此时![]() 与竖直方向交角已经大于
与竖直方向交角已经大于![]() ,杆不能达到平衡.
,杆不能达到平衡.

如图丙所示,为了达到平衡,在![]() 处,作用在圆柱上的力与法向交角不能是
处,作用在圆柱上的力与法向交角不能是![]() ,而应该变小,直到平衡时,
,而应该变小,直到平衡时,![]() 点处杆的受力方向与竖直线方向达
点处杆的受力方向与竖直线方向达![]() ,才使杆达到新的平衡。
,才使杆达到新的平衡。
下面求![]() 满足的方程.
满足的方程.
![]() .
.
由于 ,
,
最后来求![]() .
.
由图丙可知![]() ,
,
所以, ,
,
所以,  ,
,
即![]() .
.
本题是一道多点摩擦、临界分析、几何约束交织在一起的难题。
由于平衡问题的研究是学习物理的开端,很多人错误地认为平衡问题是物理中的简单问题,其实不然,以竞赛试题为例,一旦出现平衡问题,不论是复赛还是决赛,往往就是当年的难题,究其原因,平衡问题往往涉及多个对象,复杂的结构模型,多接触点的受力分析,隐晦的临界状态,不确定的可能状态,繁杂的几何关系,大量的运算等等,且不说上述各种情况同时出现,哪怕只有两三种出现在同一道试题中(如本题),答题者如不具备扎实的基础,熟练地运用知识的能力,过硬的心理素质,较强的定力,要想顺利完成解答,则无异于异想天开。