题目内容
【题目】等重的两个木块由一根不可伸长的轻绳相连,放在倾角为![]() 的斜面上,两木块与斜面的静摩擦因数分别为
的斜面上,两木块与斜面的静摩擦因数分别为![]() 和
和![]() ,已知
,已知![]() ,
,![]() 。问:绳子与斜面上的最大倾斜线之间的夹角
。问:绳子与斜面上的最大倾斜线之间的夹角![]() 应满足什么限制,它们才能在斜面上保持静止?
应满足什么限制,它们才能在斜面上保持静止?
【答案】当![]() 时,
时,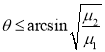 ;当
;当![]() 时,
时,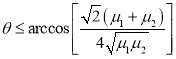 .
.
【解析】
一个物体能够静止在斜面上,其静摩擦系数应满足条件![]() .
.
由于本题已知![]() 和
和![]() ,可知
,可知![]() ,
,![]() ,木块1能单独在斜面上保持静止,而木块2不能。现在两木块由细绳连接,当木块1在高处且绳子方位适当,拉直的绳子有可能阻止木块2滑动,同时木块1不被绳子拉动。
,木块1能单独在斜面上保持静止,而木块2不能。现在两木块由细绳连接,当木块1在高处且绳子方位适当,拉直的绳子有可能阻止木块2滑动,同时木块1不被绳子拉动。
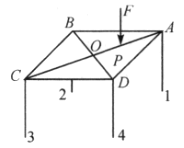
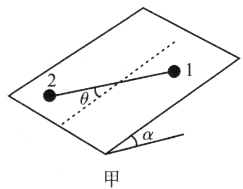
设平衡时木块如图甲所示放置。
图乙为斜面上两木块平衡时的受力图,虚线![]() 为斜面上最大倾斜线的方向。因为在
为斜面上最大倾斜线的方向。因为在![]() 足够大时,
足够大时,![]() 不能静止,将有滑动。在
不能静止,将有滑动。在![]() 很小时(例如
很小时(例如![]() ),很容易判定
),很容易判定![]() 和
和![]() 作为整体沿斜面
作为整体沿斜面![]() 方向无滑动,保持平衡。所以在
方向无滑动,保持平衡。所以在![]() 从0到足够大中间必有一个位置使
从0到足够大中间必有一个位置使![]() 处于临界状态,静摩擦力达最大。
处于临界状态,静摩擦力达最大。
我们先考虑木块2,其临界状态下由三个力作用:重力在![]() 方向的分力
方向的分力![]() ;绳中张力
;绳中张力![]() ;临界时的摩擦力
;临界时的摩擦力![]() 。由题中已知条件,有
。由题中已知条件,有![]() ,所以
,所以![]() .
.
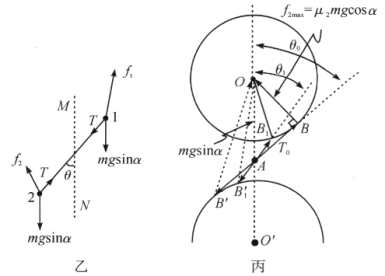
如图丙所示,作矢量图,使![]() ,方向与
,方向与![]() 平行,再以
平行,再以![]() 为圆心,
为圆心,![]() 为半径作圆,
为半径作圆,![]() 点必在圆外。过
点必在圆外。过![]() 点作圆
点作圆![]() 的切线
的切线![]() ,
,![]() 为切点。则
为切点。则![]() ,
,![]() ,方向指向
,方向指向![]() 点。因为
点。因为![]() ,所以
,所以![]() 垂直于两木块间的绳子。
垂直于两木块间的绳子。![]() 是使木块2处于临界的最大张力,对应的
是使木块2处于临界的最大张力,对应的![]() 是绳与
是绳与![]() 的最大交角。这是因为,虽然从
的最大交角。这是因为,虽然从![]() 点出发,在小于
点出发,在小于![]() 的方向画一直线与圆相交有两个交点,较远的交点对应于大的
的方向画一直线与圆相交有两个交点,较远的交点对应于大的![]() ,这个
,这个![]() 对应的最大静摩擦力使木块2有缩短绳子或有往上运动的倾向。这不符合事实,所以,
对应的最大静摩擦力使木块2有缩短绳子或有往上运动的倾向。这不符合事实,所以,![]() 是木块2保持静止的最大可能值。
是木块2保持静止的最大可能值。
再考察木块1的受力情况。为了方便,在图丙中相对于![]() 点作一个与圆
点作一个与圆![]() 对称的圆
对称的圆![]() 。木块1也受三个力作用:重力沿
。木块1也受三个力作用:重力沿![]() 方向的分力
方向的分力![]() (与木块2相同);绳中张力,大小与木块2受到的张力相等,方向相反,在图丙上对应于
(与木块2相同);绳中张力,大小与木块2受到的张力相等,方向相反,在图丙上对应于![]() 点有
点有![]() 点(当然,对应于
点(当然,对应于![]() 有
有![]() ,这由
,这由![]() 角决定);摩擦力
角决定);摩擦力![]() ,如果三力平衡,则三个力矢量可构成封闭三角形。在木块2上存在作用的绳中张力
,如果三力平衡,则三个力矢量可构成封闭三角形。在木块2上存在作用的绳中张力![]() 的条件下,
的条件下,![]() 代表作用在木块1上所必须提供的摩擦力
代表作用在木块1上所必须提供的摩擦力![]() .
.
如果木块2临界平衡时受到绳中张力较小,则![]() 也小,
也小,![]() 点变为
点变为![]() 点(圆
点(圆![]() 上)。相对于
上)。相对于![]() 对称的圆
对称的圆![]() 上必有对称的点
上必有对称的点![]() 。从图丙看出,为使质点1达平衡(即三个力矢量构成封闭三角形),所必须提供的摩擦力的最大值应等于或大于
。从图丙看出,为使质点1达平衡(即三个力矢量构成封闭三角形),所必须提供的摩擦力的最大值应等于或大于![]() 。这是由木块2处于临界平衡状态的最大
。这是由木块2处于临界平衡状态的最大![]() 角决定的。
角决定的。
我们来判定一下平衡的可能性,为此比较力:![]() 和
和![]() .
.
①若![]() ,即必须提供的
,即必须提供的![]() 大于可能提供的最大静摩擦力,在绳子与
大于可能提供的最大静摩擦力,在绳子与![]() 方向夹角为
方向夹角为![]() 时,木块1不能保持平衡。
时,木块1不能保持平衡。
②若![]() ,在绳子与
,在绳子与![]() 方向夹角为
方向夹角为![]() 时,木块1可以保持平衡。
时,木块1可以保持平衡。
如果属情况②,那么保持系统平衡的最大![]() 角是
角是![]() ;如果属情况①,我们将继续寻找这个
;如果属情况①,我们将继续寻找这个![]() 角,使
角,使![]() .系统达平衡时,绳子与
.系统达平衡时,绳子与![]() 方向夹角必须小于或等于这个
方向夹角必须小于或等于这个![]() 角.
角.
为求![]() ,先确定
,先确定![]() 与
与![]() ,由图丙得
,由图丙得
![]()
![]()
![]()
![]() .
.
又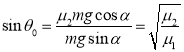 ,
,
为了在![]() 位形处系统保持平衡,如图丙所示,要求
位形处系统保持平衡,如图丙所示,要求![]() 达到的数值,可从
达到的数值,可从![]() 求得:
求得:
![]()
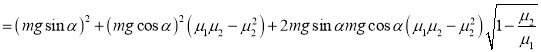
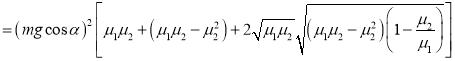
![]() .
.
又有木块1的最大静摩擦力![]() ,
,
为确定![]() 和
和![]() 间的大小关系,暂设
间的大小关系,暂设![]() ,
,
即![]() ,
,
整理得![]() .
.
在题中要求![]() 的条件下,有结论:
的条件下,有结论:
i. ![]() ,要求
,要求![]() ;
;
ii. ![]() ,要求
,要求![]() .
.
即,当![]() 时,系统达平衡的条件是绳的最大倾斜角
时,系统达平衡的条件是绳的最大倾斜角![]() ,因此,系统达平衡要求,
,因此,系统达平衡要求,
即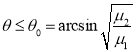 .
.
当![]() 时,在绳的倾斜角
时,在绳的倾斜角![]() 处,木块1不能平衡,而只能在
处,木块1不能平衡,而只能在![]() 的某个
的某个![]() 角才能平衡。我们来求这个临界的
角才能平衡。我们来求这个临界的![]() 角,在此
角,在此
![]() .
.
利用木块1、2达临界时的受力图丙中两个三角形![]() 和
和![]() ,得
,得
![]() ,
,
![]() .
.
两式相加、相减得
![]() ,
,
![]() .
.
联立求解得到![]() ,
,
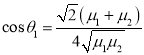 .
.
这个结果说明:当![]() 时,为使系统保持平衡,绳的倾斜角
时,为使系统保持平衡,绳的倾斜角![]() 应满足
应满足
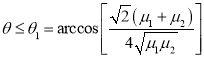 .
.
最后结论:为使系统在斜面上保持静止,绳子与斜面上的最大倾斜线之间的夹角应满足:
当![]() 时,
时,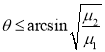 ;
;
当![]() 时,
时,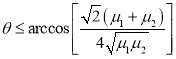 .
.