1. 下列方程属于一元二次方程的是 (
A.$2xy - 7 = 0$
B.$x^2 - 7 = 0$
C.$-7x = 0$
D.$5(x + 1) = 7^2$
B
)A.$2xy - 7 = 0$
B.$x^2 - 7 = 0$
C.$-7x = 0$
D.$5(x + 1) = 7^2$
答案:【解析】:
本题主要考察一元二次方程的定义,即只含有一个未知数,且未知数的最高次数为2的整式方程。
A选项:$2xy - 7 = 0$,此方程含有两个未知数x和y,因此不是一元二次方程。
B选项:$x^2 - 7 = 0$,此方程只含有一个未知数x,且x的最高次数为2,满足一元二次方程的定义。
C选项:$-7x = 0$,此方程只含有一个未知数x,但x的最高次数为1,因此不是一元二次方程。
D选项:$5(x + 1) = 7^2$,展开后为$5x + 5 = 49$,此方程只含有一个未知数x,但x的最高次数为1,因此不是一元二次方程。
【答案】:
B
本题主要考察一元二次方程的定义,即只含有一个未知数,且未知数的最高次数为2的整式方程。
A选项:$2xy - 7 = 0$,此方程含有两个未知数x和y,因此不是一元二次方程。
B选项:$x^2 - 7 = 0$,此方程只含有一个未知数x,且x的最高次数为2,满足一元二次方程的定义。
C选项:$-7x = 0$,此方程只含有一个未知数x,但x的最高次数为1,因此不是一元二次方程。
D选项:$5(x + 1) = 7^2$,展开后为$5x + 5 = 49$,此方程只含有一个未知数x,但x的最高次数为1,因此不是一元二次方程。
【答案】:
B
2. 方程$2x^2 - 3x = 2$的一次项系数和常数项分别是 (
A.2和2
B.$-3$和2
C.3和$-2$
D.$-3和-2$
D
)A.2和2
B.$-3$和2
C.3和$-2$
D.$-3和-2$
答案:【解析】:
本题考查一元二次方程的一般形式,即$ax^2 + bx + c = 0$(其中$a \neq 0$)的形式。
在这个形式中,$ax^2$是二次项,$bx$是一次项,$c$是常数项。
题目给出的方程是$2x^2 - 3x = 2$,为了找到一次项系数和常数项,需要先将方程化为一般形式。
将方程$2x^2 - 3x = 2$移项,得到$2x^2 - 3x - 2 = 0$。
在这个一般形式中,可以清晰地看到一次项系数是$-3$,常数项是$-2$。
【答案】:
D. $-3$和$-2$。
本题考查一元二次方程的一般形式,即$ax^2 + bx + c = 0$(其中$a \neq 0$)的形式。
在这个形式中,$ax^2$是二次项,$bx$是一次项,$c$是常数项。
题目给出的方程是$2x^2 - 3x = 2$,为了找到一次项系数和常数项,需要先将方程化为一般形式。
将方程$2x^2 - 3x = 2$移项,得到$2x^2 - 3x - 2 = 0$。
在这个一般形式中,可以清晰地看到一次项系数是$-3$,常数项是$-2$。
【答案】:
D. $-3$和$-2$。
3. 若关于$x的一元二次方程(x - a)^2 - 4 = b$有实数根,则$b$的取值范围是 (
A.$b > 4$
B.$b > -4$
C.$b \geq 4$
D.$b \geq -4$
D
)A.$b > 4$
B.$b > -4$
C.$b \geq 4$
D.$b \geq -4$
答案:解:$(x - a)^2 - 4 = b$
移项得$(x - a)^2 = b + 4$
∵一元二次方程有实数根,
∴$(x - a)^2 \geq 0$
即$b + 4 \geq 0$
解得$b \geq -4$
D
移项得$(x - a)^2 = b + 4$
∵一元二次方程有实数根,
∴$(x - a)^2 \geq 0$
即$b + 4 \geq 0$
解得$b \geq -4$
D
4. 若$x$为任意有理数,则多项式$4x - 4 - x^2$的值 (
A.一定为正数
B.一定为负数
C.不可能为正数
D.可能为任意有理数
C
)A.一定为正数
B.一定为负数
C.不可能为正数
D.可能为任意有理数
答案:【解析】:
首先,我们将多项式$4x - 4 - x^2$进行整理,得到:
$4x - 4 - x^2 = - (x^2 - 4x + 4) = - (x - 2)^2$
由于$(x - 2)^2$是一个平方项,其值总是非负的,即:
$(x - 2)^2 \geq 0$
因此,$- (x - 2)^2$的值总是非正的,即:
$- (x - 2)^2 \leq 0$
所以多项式$4x - 4 - x^2$的值不可能为正数。
【答案】:
C. 不可能为正数。
首先,我们将多项式$4x - 4 - x^2$进行整理,得到:
$4x - 4 - x^2 = - (x^2 - 4x + 4) = - (x - 2)^2$
由于$(x - 2)^2$是一个平方项,其值总是非负的,即:
$(x - 2)^2 \geq 0$
因此,$- (x - 2)^2$的值总是非正的,即:
$- (x - 2)^2 \leq 0$
所以多项式$4x - 4 - x^2$的值不可能为正数。
【答案】:
C. 不可能为正数。
5. 若关于$x的一元二次方程ax^2 + bx + 1 = 0$的一个根是1,则$2024 - a - b$的值是 (
A.2025
B.2023
C.2024
D.2022
A
)A.2025
B.2023
C.2024
D.2022
答案:解:
∵关于$x$的一元二次方程$ax^2 + bx + 1 = 0$的一个根是$1$,
∴将$x = 1$代入方程得:$a×1^2 + b×1 + 1 = 0$,
即$a + b + 1 = 0$,
∴$a + b = -1$,
则$2024 - a - b = 2024 - (a + b) = 2024 - (-1) = 2025$。
A
∵关于$x$的一元二次方程$ax^2 + bx + 1 = 0$的一个根是$1$,
∴将$x = 1$代入方程得:$a×1^2 + b×1 + 1 = 0$,
即$a + b + 1 = 0$,
∴$a + b = -1$,
则$2024 - a - b = 2024 - (a + b) = 2024 - (-1) = 2025$。
A
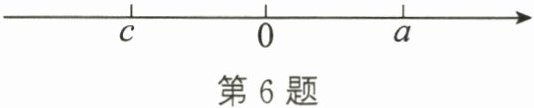
6. 已知关于$x的一元二次方程ax^2 - x + c = 0$,其中$a$,$c$在数轴上的对应点的位置如图所示,则这个方程的根的情况是 (
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
C
)
A.没有实数根
B.有两个相等的实数根
C.有两个不相等的实数根
D.无法确定
答案:解:由数轴可知,$a > 0$,$c < 0$。
对于一元二次方程$ax^2 - x + c = 0$,判别式$\Delta = (-1)^2 - 4ac = 1 - 4ac$。
因为$a > 0$,$c < 0$,所以$ac < 0$,则$-4ac > 0$,故$\Delta = 1 - 4ac > 1 > 0$。
所以方程有两个不相等的实数根。
答案:C
对于一元二次方程$ax^2 - x + c = 0$,判别式$\Delta = (-1)^2 - 4ac = 1 - 4ac$。
因为$a > 0$,$c < 0$,所以$ac < 0$,则$-4ac > 0$,故$\Delta = 1 - 4ac > 1 > 0$。
所以方程有两个不相等的实数根。
答案:C
7. 把一根长为2 m的绳子分成两段,使较长一段的长的平方等于较短一段的长与原绳长的积. 设较长一段的长为$x$ m,根据题意,可列方程为 (
A.$x^2 = 2(2 - x)$
B.$x^2 = 2(2 + x)$
C.$(2 - x)^2 = 2x$
D.$x^2 = 2 - x$
A
)A.$x^2 = 2(2 - x)$
B.$x^2 = 2(2 + x)$
C.$(2 - x)^2 = 2x$
D.$x^2 = 2 - x$
答案:解:设较长一段的长为$x$m,则较短一段的长为$(2 - x)$m。
根据题意,较长一段的长的平方等于较短一段的长与原绳长的积,可列方程为:$x^2 = 2(2 - x)$。
答案:A
根据题意,较长一段的长的平方等于较短一段的长与原绳长的积,可列方程为:$x^2 = 2(2 - x)$。
答案:A
8. 已知实数a,b,且$a \neq b,$又a,b满足$a^2 = 3a + 1,b^2 = 3b + 1,$则$a^2 + b^2$的值为 (
A.9
B.10
C.11
D.12
C
)A.9
B.10
C.11
D.12
答案:【解析】:
本题主要考查了一元二次方程的根与系数的关系以及代数式的化简。
根据题目条件,$a$ 和 $b$ 是方程 $x^2 - 3x - 1 = 0$ 的两个不相等的实数根。
根据一元二次方程的根与系数的关系,我们有:
根的和:$a + b = -\frac{-3}{1} = 3$,
根的积:$ab = \frac{-1}{1} = -1$,
接下来,我们需要求 $a^2 + b^2$ 的值。
根据平方和公式,我们有:
$a^2 + b^2 = (a + b)^2 - 2ab$,
将 $a + b = 3$ 和 $ab = -1$ 代入上式,得到:
$a^2 + b^2 = 3^2 - 2 × (-1) = 9 + 2 = 11$。
【答案】:
C. $11$。
本题主要考查了一元二次方程的根与系数的关系以及代数式的化简。
根据题目条件,$a$ 和 $b$ 是方程 $x^2 - 3x - 1 = 0$ 的两个不相等的实数根。
根据一元二次方程的根与系数的关系,我们有:
根的和:$a + b = -\frac{-3}{1} = 3$,
根的积:$ab = \frac{-1}{1} = -1$,
接下来,我们需要求 $a^2 + b^2$ 的值。
根据平方和公式,我们有:
$a^2 + b^2 = (a + b)^2 - 2ab$,
将 $a + b = 3$ 和 $ab = -1$ 代入上式,得到:
$a^2 + b^2 = 3^2 - 2 × (-1) = 9 + 2 = 11$。
【答案】:
C. $11$。
目录查找(点击展开或折叠章节目录)
X
