1. 使式子$\sqrt {2x+1}$在实数范围内有意义的x的取值范围是
$x \geq -\frac{1}{2}$
.答案:【解析】:
为了使$\sqrt{2x+1}$在实数范围内有意义,被开方数$2x+1$必须是非负数。
因此,我们设置不等式:
$2x + 1 \geq 0$
解这个不等式,我们得到:
$2x \geq -1$
$x \geq -\frac{1}{2}$
【答案】:
$x \geq -\frac{1}{2}$
为了使$\sqrt{2x+1}$在实数范围内有意义,被开方数$2x+1$必须是非负数。
因此,我们设置不等式:
$2x + 1 \geq 0$
解这个不等式,我们得到:
$2x \geq -1$
$x \geq -\frac{1}{2}$
【答案】:
$x \geq -\frac{1}{2}$
2. 在一次函数$y= (2-k)x+1$中,若$y随x$的增大而增大,则$k$的取值范围为______
$k<2$
.答案:【解析】:对于一次函数$y = mx + b$($m$、$b$为常数,$m\neq0$),当$m>0$时,$y$随$x$的增大而增大。在函数$y=(2 - k)x + 1$中,斜率$m = 2 - k$。因为$y$随$x$的增大而增大,所以$2 - k>0$,解这个不等式可得$k<2$。
【答案】:$k<2$
【答案】:$k<2$
3. 在一个四边形中,最多能有
3
个锐角,最多能有3
个钝角.答案:【解析】:对于四边形中锐角的个数,因为锐角是小于$90^{\circ}$的角,假设四边形有$4$个锐角,那么四个内角之和会小于$4×90^{\circ}=360^{\circ}$,这与四边形内角和是$360^{\circ}$矛盾;若有$3$个锐角,设这$3$个锐角都接近$90^{\circ}$,比如都为$89^{\circ}$,则第四个角为$360^{\circ}-3×89^{\circ}=360^{\circ}-267^{\circ}=93^{\circ}$,是合理的,所以最多有$3$个锐角。
对于钝角的个数,钝角是大于$90^{\circ}$小于$180^{\circ}$的角,假设四边形有$4$个钝角,那么四个内角之和会大于$4×90^{\circ}=360^{\circ}$且小于$4×180^{\circ}=720^{\circ}$,但四边形内角和固定为$360^{\circ}$,$4$个钝角之和必然大于$360^{\circ}$,矛盾;若有$3$个钝角,设这$3$个钝角都接近$180^{\circ}$,比如都为$91^{\circ}$,则第四个角为$360^{\circ}-3×91^{\circ}=360^{\circ}-273^{\circ}=87^{\circ}$,是合理的,所以最多有$3$个钝角。
【答案】:3,3
对于钝角的个数,钝角是大于$90^{\circ}$小于$180^{\circ}$的角,假设四边形有$4$个钝角,那么四个内角之和会大于$4×90^{\circ}=360^{\circ}$且小于$4×180^{\circ}=720^{\circ}$,但四边形内角和固定为$360^{\circ}$,$4$个钝角之和必然大于$360^{\circ}$,矛盾;若有$3$个钝角,设这$3$个钝角都接近$180^{\circ}$,比如都为$91^{\circ}$,则第四个角为$360^{\circ}-3×91^{\circ}=360^{\circ}-273^{\circ}=87^{\circ}$,是合理的,所以最多有$3$个钝角。
【答案】:3,3
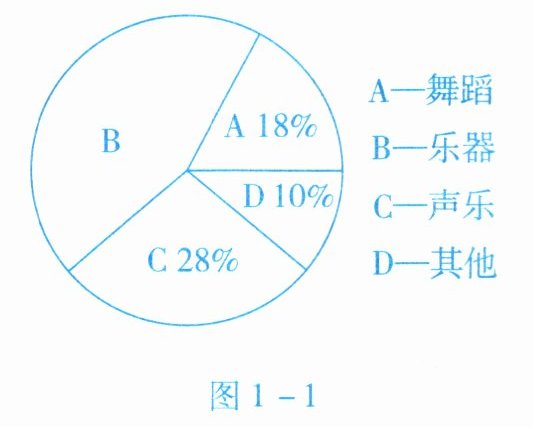
4. 某班围绕“舞蹈、乐器、声乐、其他项目中,你最喜欢哪项活动(每人只限选一项)”的问题,对全班50名学生进行问卷调查,调查结果如图1-1所示的扇形统计图,则该班喜欢乐器的学生有
22
名.
答案:【解析】:根据扇形统计图可知,喜欢乐器的学生所占比例为:
$1 - 18\% - 28\% - 10\% = 44\%$。
该班学生总人数为$50$名,所以喜欢乐器的学生人数为:
$50× 44\% = 50×0.44 = 22$(名)。
【答案】:$22$
$1 - 18\% - 28\% - 10\% = 44\%$。
该班学生总人数为$50$名,所以喜欢乐器的学生人数为:
$50× 44\% = 50×0.44 = 22$(名)。
【答案】:$22$
5. 如图$1-2$所示,在矩形$ABCD$中,对角线$AC$,$BD相交于点O$,点$E$,$F分别是AO$,$AD$的中点. 若$AB= 6cm$,$BC= 8cm$,则$\triangle AEF$的周长为______
9
$cm$.答案:【解析】:
首先,由于$ABCD$是矩形,所以根据勾股定理,有$AC = \sqrt{AB^2 + BC^2} = \sqrt{6^2 + 8^2} = 10 \text{ cm}$。
由于$O$是对角线$AC$和$BD$的交点,根据矩形的性质,$O$是$AC$的中点,所以$AO = \frac{AC}{2} = 5 \text{ cm}$。
点$E$是$AO$的中点,所以$AE = \frac{AO}{2} = 2.5 \text{ cm}$。
点$F$是$AD$的中点,由于$AD = BC = 8 \text{ cm}$,所以$AF = \frac{AD}{2} = 4 \text{ cm}$。
由于$E$和$F$分别是$AO$和$AD$的中点,根据中位线的性质,$EF$是$\triangle AOD$的中位线,所以$EF = \frac{1}{2}OD = \frac{1}{2} × \frac{1}{2}BD = \frac{1}{4}AC = 2.5 \text{ cm}$(这里用到了$OD = \frac{1}{2}BD$和$BD = AC$)。
最后,$\triangle AEF$的周长为$AE + AF + EF = 2.5 + 4 + 2.5 = 9 \text{ cm}$。
【答案】:9
首先,由于$ABCD$是矩形,所以根据勾股定理,有$AC = \sqrt{AB^2 + BC^2} = \sqrt{6^2 + 8^2} = 10 \text{ cm}$。
由于$O$是对角线$AC$和$BD$的交点,根据矩形的性质,$O$是$AC$的中点,所以$AO = \frac{AC}{2} = 5 \text{ cm}$。
点$E$是$AO$的中点,所以$AE = \frac{AO}{2} = 2.5 \text{ cm}$。
点$F$是$AD$的中点,由于$AD = BC = 8 \text{ cm}$,所以$AF = \frac{AD}{2} = 4 \text{ cm}$。
由于$E$和$F$分别是$AO$和$AD$的中点,根据中位线的性质,$EF$是$\triangle AOD$的中位线,所以$EF = \frac{1}{2}OD = \frac{1}{2} × \frac{1}{2}BD = \frac{1}{4}AC = 2.5 \text{ cm}$(这里用到了$OD = \frac{1}{2}BD$和$BD = AC$)。
最后,$\triangle AEF$的周长为$AE + AF + EF = 2.5 + 4 + 2.5 = 9 \text{ cm}$。
【答案】:9
1. 矩形的两条对角线的夹角是$120^{\circ }$,较短的边长是$4cm$,则其较长的边长是(
A.$8\sqrt {3}cm$
B.$8cm$
C.$4\sqrt {3}cm$
D.$4cm$
C
)A.$8\sqrt {3}cm$
B.$8cm$
C.$4\sqrt {3}cm$
D.$4cm$
答案:【解析】:在矩形中,对角线相等且互相平分,所以两条对角线与矩形两边构成的三角形中,两条对角线的一半相等。已知两条对角线的夹角是$120^{\circ}$,则其邻补角为$60^{\circ}$。较短的边长与两条对角线的一半构成一个等边三角形(因为夹角为$60^{\circ}$且两边相等),所以对角线的一半等于较短边长$4cm$,则对角线长为$8cm$。
设较长的边长为$x cm$,根据勾股定理,较短边、较长边与对角线构成直角三角形,可得:$4^{2} + x^{2} = 8^{2}$,即$16 + x^{2} = 64$,解得$x^{2} = 48$,$x = 4\sqrt{3}$(负值舍去)。
【答案】:C
设较长的边长为$x cm$,根据勾股定理,较短边、较长边与对角线构成直角三角形,可得:$4^{2} + x^{2} = 8^{2}$,即$16 + x^{2} = 64$,解得$x^{2} = 48$,$x = 4\sqrt{3}$(负值舍去)。
【答案】:C
2. 下列计算错误的是(
A.$\sqrt {2}\cdot \sqrt {3}= \sqrt {6}$
B.$\sqrt {2}+\sqrt {3}= \sqrt {6}$
C.$\sqrt {12}÷ \sqrt {3}= 2$
D.$\sqrt {8}= 2\sqrt {2}$
B
)A.$\sqrt {2}\cdot \sqrt {3}= \sqrt {6}$
B.$\sqrt {2}+\sqrt {3}= \sqrt {6}$
C.$\sqrt {12}÷ \sqrt {3}= 2$
D.$\sqrt {8}= 2\sqrt {2}$
答案:【解析】:逐一分析各选项:
选项A:根据二次根式乘法法则,$\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}$($a\geq0$,$b\geq0$),所以$\sqrt{2} \cdot \sqrt{3} = \sqrt{2×3} = \sqrt{6}$,计算正确。
选项B:$\sqrt{2}$和$\sqrt{3}$不是同类二次根式,不能直接合并,$\sqrt{2} + \sqrt{3}$已是最简形式,不能等于$\sqrt{6}$,计算错误。
选项C:根据二次根式除法法则,$\sqrt{a} ÷ \sqrt{b} = \sqrt{\frac{a}{b}}$($a\geq0$,$b>0$),所以$\sqrt{12} ÷ \sqrt{3} = \sqrt{\frac{12}{3}} = \sqrt{4} = 2$,计算正确。
选项D:$\sqrt{8} = \sqrt{4×2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2}$,计算正确。
综上,计算错误的是选项B。
【答案】:B
选项A:根据二次根式乘法法则,$\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}$($a\geq0$,$b\geq0$),所以$\sqrt{2} \cdot \sqrt{3} = \sqrt{2×3} = \sqrt{6}$,计算正确。
选项B:$\sqrt{2}$和$\sqrt{3}$不是同类二次根式,不能直接合并,$\sqrt{2} + \sqrt{3}$已是最简形式,不能等于$\sqrt{6}$,计算错误。
选项C:根据二次根式除法法则,$\sqrt{a} ÷ \sqrt{b} = \sqrt{\frac{a}{b}}$($a\geq0$,$b>0$),所以$\sqrt{12} ÷ \sqrt{3} = \sqrt{\frac{12}{3}} = \sqrt{4} = 2$,计算正确。
选项D:$\sqrt{8} = \sqrt{4×2} = \sqrt{4} \cdot \sqrt{2} = 2\sqrt{2}$,计算正确。
综上,计算错误的是选项B。
【答案】:B
目录查找(点击展开或折叠章节目录)
X
