题目内容
 如图所示,体重是800N的工人利用滑轮组把浸没在水中的物体A提升出水面.物体A浸没在水中匀速上升时,滑轮组的机械效率为η1=70%.物体A被完全提出水面后匀速上升时,滑轮组的机械效率为η2=85%,此时水平地面对工人的支持力为FN2=200N.不计滑轮轴摩擦和绳重.求:
如图所示,体重是800N的工人利用滑轮组把浸没在水中的物体A提升出水面.物体A浸没在水中匀速上升时,滑轮组的机械效率为η1=70%.物体A被完全提出水面后匀速上升时,滑轮组的机械效率为η2=85%,此时水平地面对工人的支持力为FN2=200N.不计滑轮轴摩擦和绳重.求:
(1)物体A受到的重力GA;
(2)物体A浸没在水中时,水平地面对工人的支持力FN1;
(3)物体A的密度ρA.
已知:G人=800N FN2=200N n=2 η2=85% η1=70%
求:(1)GA=?(2)FN1=?(3)ρA=?
解:
(1)物体A被提出水面后,
以工人为研究对象受力分析如图1.

∵FN2+FT2=G人
∴绳子对人的拉力是FT2=G人-FN2=800N-200N=600N,
绳子对人的拉力是F2=FT2=600N;
以物体A和动滑轮为研究对象受力分析如图2.

GA+G轮=2F2=2×600N=1200N;
∵η2=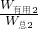 =
= =
= =
= ,
,
∴物体A受到的重力为GA=η22F2=85%×1200N=1020N;
(2)∵F= (G+G轮),
(G+G轮),
∴动滑轮的重力为G轮=2F2-GA=1200N-1020N=180N,
此时滑轮组的机械效率为η1= =
= =
= =70%,
=70%,
∴物体受到的浮力为F浮=GA- G轮=1020N-
G轮=1020N- ×180N=600N;
×180N=600N;
物体A在水中时,以物体A和动滑轮为研究对象受力分析如图3.

2F1+F浮=GA+G轮
F1= (GA+G轮-F浮)=
(GA+G轮-F浮)= (1200N-600N)=300N,
(1200N-600N)=300N,
地面对人的支持力FN1=G人-FT1=800N-300N=500N;
(3)∵G=mg=ρVg,
F浮=ρ液gV排,
物体A浸没在水中,VA=V排
由上得 =
=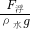 ,
,
∴物体的密度为ρA= ρ水=
ρ水= ×1×103kg/m3=1.7×103kg/m3.
×1×103kg/m3=1.7×103kg/m3.
答:
(1)物体A受到的重力为1020N;
(2)地面对人的支持力为500N;
(3)物体的密度为1.7×103kg/m3.
分析:(1)物体A被提出水面后,人受到三个力的作用:重力、地面支持力和绳子的拉力,已知重力、地面支持力,可以得到绳子的拉力,由于力的作用是相互的,可以得到人对绳子是拉力;由图知,作用在动滑轮上的绳子有2段,根据滑轮组的特点可以得到物体A的重力与动滑轮的重力与拉力的关系;不计绳重和摩擦,拉力对动滑轮和物体A做的功为总功,对物体A做的功为有用功,利用机械效率变形公式得到物体A的重力;
(2)已知物重和拉力,可以得到动滑轮的重力;物体浸没在水中时,有用功是克服物重与浮力之差做的功;总功是作用在绳子末端的拉力做的功;已知物体浸没在水中时滑轮组的机械效率、物重、动滑轮重,可以得到物体受到的浮力,进一步得到手对绳子是拉力,由于力的作用是相互的,绳子对人的拉力得解;已知人的体重、绳子对人的拉力,可以得到地面对人的支持力;
(3)物体浸没时,排开水的体积等于物体的体积,已知物重、浮力和水的密度,利用阿基米德原理和重力的计算公式得到物体的密度.
点评:本题考查力学综合计算分析,是每年固定的必考题目,对应知识点经常出现在各种综合考试的最后一题中,属于热点问题,但是此题的创新之处在于在物体所在位置这个决定性的关键问题上给考生设置了一个陷阱,要求考生对滑轮组的特点及机械效率的变化理解透彻,并且要具有很强的临场应变能力和分析能力.
求:(1)GA=?(2)FN1=?(3)ρA=?
解:
(1)物体A被提出水面后,
以工人为研究对象受力分析如图1.

∵FN2+FT2=G人
∴绳子对人的拉力是FT2=G人-FN2=800N-200N=600N,
绳子对人的拉力是F2=FT2=600N;
以物体A和动滑轮为研究对象受力分析如图2.

GA+G轮=2F2=2×600N=1200N;
∵η2=
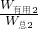 =
= =
= =
= ,
,∴物体A受到的重力为GA=η22F2=85%×1200N=1020N;
(2)∵F=
 (G+G轮),
(G+G轮),∴动滑轮的重力为G轮=2F2-GA=1200N-1020N=180N,
此时滑轮组的机械效率为η1=
 =
= =
= =70%,
=70%,∴物体受到的浮力为F浮=GA-
 G轮=1020N-
G轮=1020N- ×180N=600N;
×180N=600N;物体A在水中时,以物体A和动滑轮为研究对象受力分析如图3.

2F1+F浮=GA+G轮
F1=
 (GA+G轮-F浮)=
(GA+G轮-F浮)= (1200N-600N)=300N,
(1200N-600N)=300N,地面对人的支持力FN1=G人-FT1=800N-300N=500N;
(3)∵G=mg=ρVg,
F浮=ρ液gV排,
物体A浸没在水中,VA=V排
由上得
 =
=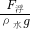 ,
,∴物体的密度为ρA=
 ρ水=
ρ水= ×1×103kg/m3=1.7×103kg/m3.
×1×103kg/m3=1.7×103kg/m3.答:
(1)物体A受到的重力为1020N;
(2)地面对人的支持力为500N;
(3)物体的密度为1.7×103kg/m3.
分析:(1)物体A被提出水面后,人受到三个力的作用:重力、地面支持力和绳子的拉力,已知重力、地面支持力,可以得到绳子的拉力,由于力的作用是相互的,可以得到人对绳子是拉力;由图知,作用在动滑轮上的绳子有2段,根据滑轮组的特点可以得到物体A的重力与动滑轮的重力与拉力的关系;不计绳重和摩擦,拉力对动滑轮和物体A做的功为总功,对物体A做的功为有用功,利用机械效率变形公式得到物体A的重力;
(2)已知物重和拉力,可以得到动滑轮的重力;物体浸没在水中时,有用功是克服物重与浮力之差做的功;总功是作用在绳子末端的拉力做的功;已知物体浸没在水中时滑轮组的机械效率、物重、动滑轮重,可以得到物体受到的浮力,进一步得到手对绳子是拉力,由于力的作用是相互的,绳子对人的拉力得解;已知人的体重、绳子对人的拉力,可以得到地面对人的支持力;
(3)物体浸没时,排开水的体积等于物体的体积,已知物重、浮力和水的密度,利用阿基米德原理和重力的计算公式得到物体的密度.
点评:本题考查力学综合计算分析,是每年固定的必考题目,对应知识点经常出现在各种综合考试的最后一题中,属于热点问题,但是此题的创新之处在于在物体所在位置这个决定性的关键问题上给考生设置了一个陷阱,要求考生对滑轮组的特点及机械效率的变化理解透彻,并且要具有很强的临场应变能力和分析能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
小明学过有关机械效率的知识后,提出了一个问题:斜面的机械效率与斜面的倾斜程度有没有关系?针对这个问题他做了探究实验,实验装置如图所示,并记录实验数据如下表:

(1)根据表中数据,可求出第三次实验的机械效率为 .
(2)通过对上述实验数据的分析,你认为斜面省力情况与斜面倾斜程度的关系是 .
(3)通过对上述实验数据的分析,你对斜面机械效率的问题可获得的初步结论是:
.

| 实验次数 | 斜面的 倾斜程度 |
物体重 G/N |
物体上升高度h/m | 沿斜面拉力 F/N |
物体移动距离S/m | 有用功 W有/J |
总功 W总/J |
机械效率η |
| 1 | 较缓 | 5.0 | 0.10 | 1.6 | 0.50 | 0.50 | 0.80 | 63% |
| 2 | 较陡 | 5.0 | 0.15 | 2.2 | 0.50 | 0.75 | 1.1 | 68% |
| 3 | 最陡 | 5.0 | 0.25 | 3.1 | 0.50 |
(2)通过对上述实验数据的分析,你认为斜面省力情况与斜面倾斜程度的关系是
(3)通过对上述实验数据的分析,你对斜面机械效率的问题可获得的初步结论是:
 如图所示,斜面长为2m,高为1m,A物体重为8N,B物体重为5N,恰好能使A沿着斜面匀速向上运动,那么斜面的机械效率是
如图所示,斜面长为2m,高为1m,A物体重为8N,B物体重为5N,恰好能使A沿着斜面匀速向上运动,那么斜面的机械效率是 用斜面来提升重物时,如图所示:斜面长lm,高0.2m,使用时机械效率为80%,将物体从斜面底端匀速拉到斜面顶端,需要用平行于斜面的力2.5N,那么总功是
用斜面来提升重物时,如图所示:斜面长lm,高0.2m,使用时机械效率为80%,将物体从斜面底端匀速拉到斜面顶端,需要用平行于斜面的力2.5N,那么总功是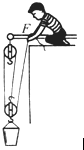 A.某工地用如图所示的滑轮组匀速提升600N的重物,在重物上升0.2m的过程中,滑轮组的机械效率为80%(不计绳重以及滑轮轮与轴之间的摩擦,).则:
A.某工地用如图所示的滑轮组匀速提升600N的重物,在重物上升0.2m的过程中,滑轮组的机械效率为80%(不计绳重以及滑轮轮与轴之间的摩擦,).则: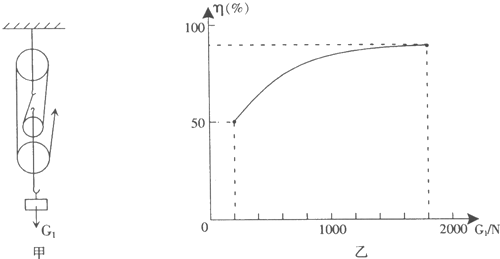
 如图所示,拉力F=125N,在10s内将重物匀速提升2m,滑轮组的机械效率是80%,则下列说法正确的是( )
如图所示,拉力F=125N,在10s内将重物匀速提升2m,滑轮组的机械效率是80%,则下列说法正确的是( )