题目内容
 一个质量为70kg的工人,用如图所示的装置(包括滑轮组及装砖的托板)提升一堆砖.已知装砖的托板重200N,每块砖重100N.滑轮的摩擦和绳重均可忽略不计,当工人匀速提升10块砖时,此装置的机械效率为80%.那么,该人站在地面上用此装置提升这些砖的过程中,此装置的机械效率最高可达到 ________.(取g=10N/kg,结果保留1位小数)
一个质量为70kg的工人,用如图所示的装置(包括滑轮组及装砖的托板)提升一堆砖.已知装砖的托板重200N,每块砖重100N.滑轮的摩擦和绳重均可忽略不计,当工人匀速提升10块砖时,此装置的机械效率为80%.那么,该人站在地面上用此装置提升这些砖的过程中,此装置的机械效率最高可达到 ________.(取g=10N/kg,结果保留1位小数)
81.5%
分析:由滑轮组装置可知承担物重的绳子股数n=2,重物被提升h,则拉力端移动的距离s=2h,
(1)求出10块砖重G砖和升高的高度h求出有用功;
知道滑轮组的机械效率,根据机械效率的公式求出总功;
而总功等于有用功与额外功之和,可以求出额外功;
不计滑轮的摩擦和绳重,使用滑轮组做的额外功就是提升动滑轮做的功W额=(G轮+G板)h,可以求出动滑轮重;
(2)当人站在地面上用此装置提升这些砖的过程中,使用最大拉力不能超过人自重(否则人会被提起),
假设F′=G人,根据F= (G轮+G板+G砖)求出最大砖重G砖′,求出有用功W有′=G砖′h,总功W总′=F′s,再利用机械效率的公式求此时的机械效率.
(G轮+G板+G砖)求出最大砖重G砖′,求出有用功W有′=G砖′h,总功W总′=F′s,再利用机械效率的公式求此时的机械效率.
解答:由图知,n=2,若砖被提升h,则拉力端移动的距离s=2h,
(1)当工人匀速提升10块砖时,
W有用=G砖×h=100N×10×h=1000N×h,
∵η= ,
,
∴W总=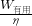 =
= ,
,
∵W总=W有用+W额,
∴W额=W总-W有用= -1000N×h=250N×h;-----①
-1000N×h=250N×h;-----①
∵不计滑轮的摩擦和绳重,
∴使用滑轮组做的额外功:
W额=(G轮+G板)h=(G轮+200N)h,-------②
由①②得:
(G轮+200N)h=250N×h
解得:G轮=50N;
(2)由题知,人使用的最大拉力:
F大=G人=mg=70kg×10N/kg=700N,
∵F大= (G轮+G板+G砖)=
(G轮+G板+G砖)= (50N+200N+G砖)=700N,
(50N+200N+G砖)=700N,
能提升的最大砖重:
G砖=1150N,
∵每块砖重100N,
∴最多能提升砖的数量为11块,
∴能提升的最大砖重:
G砖′=1100N,
此时拉力F′= (G轮+G板+G砖′)=
(G轮+G板+G砖′)= (50N+200N+1100N)=675N,
(50N+200N+1100N)=675N,
W有用′=G砖′×h=1100N×h,
W总′=F′s=675N×2h,
η′=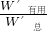 =
= =81.5%.
=81.5%.
故答案为:81.5%.
点评:本题考查了使用滑轮组时有用功、总功、机械效率的计算方法,
不计滑轮的摩擦和绳重,用好“使用滑轮组做的额外功W额=(G轮+G板)h,拉力F= (G轮+G板+G砖)”是本题的关键.
(G轮+G板+G砖)”是本题的关键.
分析:由滑轮组装置可知承担物重的绳子股数n=2,重物被提升h,则拉力端移动的距离s=2h,
(1)求出10块砖重G砖和升高的高度h求出有用功;
知道滑轮组的机械效率,根据机械效率的公式求出总功;
而总功等于有用功与额外功之和,可以求出额外功;
不计滑轮的摩擦和绳重,使用滑轮组做的额外功就是提升动滑轮做的功W额=(G轮+G板)h,可以求出动滑轮重;
(2)当人站在地面上用此装置提升这些砖的过程中,使用最大拉力不能超过人自重(否则人会被提起),
假设F′=G人,根据F=
 (G轮+G板+G砖)求出最大砖重G砖′,求出有用功W有′=G砖′h,总功W总′=F′s,再利用机械效率的公式求此时的机械效率.
(G轮+G板+G砖)求出最大砖重G砖′,求出有用功W有′=G砖′h,总功W总′=F′s,再利用机械效率的公式求此时的机械效率.解答:由图知,n=2,若砖被提升h,则拉力端移动的距离s=2h,
(1)当工人匀速提升10块砖时,
W有用=G砖×h=100N×10×h=1000N×h,
∵η=
 ,
,∴W总=
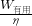 =
= ,
,∵W总=W有用+W额,
∴W额=W总-W有用=
 -1000N×h=250N×h;-----①
-1000N×h=250N×h;-----①∵不计滑轮的摩擦和绳重,
∴使用滑轮组做的额外功:
W额=(G轮+G板)h=(G轮+200N)h,-------②
由①②得:
(G轮+200N)h=250N×h
解得:G轮=50N;
(2)由题知,人使用的最大拉力:
F大=G人=mg=70kg×10N/kg=700N,
∵F大=
 (G轮+G板+G砖)=
(G轮+G板+G砖)= (50N+200N+G砖)=700N,
(50N+200N+G砖)=700N,能提升的最大砖重:
G砖=1150N,
∵每块砖重100N,
∴最多能提升砖的数量为11块,
∴能提升的最大砖重:
G砖′=1100N,
此时拉力F′=
 (G轮+G板+G砖′)=
(G轮+G板+G砖′)= (50N+200N+1100N)=675N,
(50N+200N+1100N)=675N,W有用′=G砖′×h=1100N×h,
W总′=F′s=675N×2h,
η′=
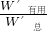 =
= =81.5%.
=81.5%.故答案为:81.5%.
点评:本题考查了使用滑轮组时有用功、总功、机械效率的计算方法,
不计滑轮的摩擦和绳重,用好“使用滑轮组做的额外功W额=(G轮+G板)h,拉力F=
 (G轮+G板+G砖)”是本题的关键.
(G轮+G板+G砖)”是本题的关键. 
练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
 水平地面上有一个质量为70kg的箱子.小刚用70N的水平推力使它在3s内匀速前进了3.6m.此后小刚停止推箱子.箱子又经过1.2s向前滑动了72cm停下来.请问:
水平地面上有一个质量为70kg的箱子.小刚用70N的水平推力使它在3s内匀速前进了3.6m.此后小刚停止推箱子.箱子又经过1.2s向前滑动了72cm停下来.请问: (2009?延庆县一模)一个质量为70kg的工人,用右所示的装置提升一堆相同的金属块.若动滑轮重50N,装金属块的托板重100N,每块金属块重100N.不计摩擦和绳重,当工人匀速提升金属块时,此装置的机械效率最高可达到
(2009?延庆县一模)一个质量为70kg的工人,用右所示的装置提升一堆相同的金属块.若动滑轮重50N,装金属块的托板重100N,每块金属块重100N.不计摩擦和绳重,当工人匀速提升金属块时,此装置的机械效率最高可达到 一个质量为70kg的工人,用如图所示的装置(包括滑轮组及装砖的托板)提升一堆砖.已知装砖的托板重200N,每块砖重100N.滑轮的摩擦和绳重均可忽略不计,当工人匀速提升10块砖时,此装置的机械效率为80%.那么,该人站在地面上用此装置提升这些砖的过程中,此装置的机械效率最高可达到
一个质量为70kg的工人,用如图所示的装置(包括滑轮组及装砖的托板)提升一堆砖.已知装砖的托板重200N,每块砖重100N.滑轮的摩擦和绳重均可忽略不计,当工人匀速提升10块砖时,此装置的机械效率为80%.那么,该人站在地面上用此装置提升这些砖的过程中,此装置的机械效率最高可达到
 (2009?朝阳区一模)一个质量为70kg的工人,用图所示的装置(包括滑轮组及装石板的托板)提升石板.已知托板重200N,每块石板重100N,滑轮的摩擦和绳重均可忽略不计,当工人在4s内匀速提升10块石板升高2m时,此装置的机械效率为80%.那么,该工人站在地面上用此装置提升石板的过程中,下列有关说法错误的是(取g=10N/kg)( )
(2009?朝阳区一模)一个质量为70kg的工人,用图所示的装置(包括滑轮组及装石板的托板)提升石板.已知托板重200N,每块石板重100N,滑轮的摩擦和绳重均可忽略不计,当工人在4s内匀速提升10块石板升高2m时,此装置的机械效率为80%.那么,该工人站在地面上用此装置提升石板的过程中,下列有关说法错误的是(取g=10N/kg)( )