题目内容
在某铁路与公路交叉的道口处安装的自动栏木装置如图所示,当高速列车到达A点时,道口公路上应显示红灯,警告未越过停车线的汽车迅速制动,而越过停车线的汽车能在列车到达道口前安全通过道口.已知A点到道口的距离L为2400m,高速列车的速度v1=144km/h.汽车驶至停车线时立即制动后滑行的距离是s=6m,道口宽度s=26m,汽车长l=18m.若道口栏木关闭时间t1=15s,为保障安全需要多加时间t2=20s,问此时该汽车至少要以多大的速度才能安全通过道口?
【答案】分析:当汽车恰好越过道口,即通过的路程等于s+s+L,汽车用的时间加上道口栏木关闭时间、为保障安全多加的时间等于列车行驶时间,据此列方程求解.
解答:解:设汽车的最大速度为v.
∵v= ,
,
∴t=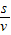 ,
,
由题知,t汽车+t1+t2=t列车,
即: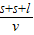 +t1+t2=
+t1+t2=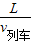 ,
,
代入数据:
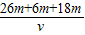 +15s+20s=
+15s+20s=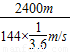 ,
,
解得:v=2m/s.
答:此时该汽车至少要以2m/s的速度才能安全通过道口.
点评:本题涉及两个物体的运动情况,关键分析两个物体之间的关系,本题关键是利用时间相等列出方程求解.
解答:解:设汽车的最大速度为v.
∵v=
 ,
,∴t=
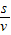 ,
,由题知,t汽车+t1+t2=t列车,
即:
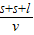 +t1+t2=
+t1+t2=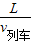 ,
,代入数据:
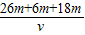 +15s+20s=
+15s+20s=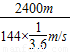 ,
,解得:v=2m/s.
答:此时该汽车至少要以2m/s的速度才能安全通过道口.
点评:本题涉及两个物体的运动情况,关键分析两个物体之间的关系,本题关键是利用时间相等列出方程求解.

练习册系列答案
相关题目
 在某铁路与公路交叉的道口处安装的自动栏木装置如图所示,当高速列车到达A点时,道口公路上应显示红灯,警告未越过停车线的汽车迅速制动,而越过停车线的汽车能在列车到达道口前安全通过道口.已知A点到道口的距离L为2400m,高速列车的速度v1=144km/h.汽车驶至停车线时立即制动后滑行的距离是s0=6m,道口宽度s=26m,汽车长l=18m.若道口栏木关闭时间t1=15s,为保障安全需要多加时间t2=20s,问此时该汽车至少要以多大的速度才能安全通过道口?
在某铁路与公路交叉的道口处安装的自动栏木装置如图所示,当高速列车到达A点时,道口公路上应显示红灯,警告未越过停车线的汽车迅速制动,而越过停车线的汽车能在列车到达道口前安全通过道口.已知A点到道口的距离L为2400m,高速列车的速度v1=144km/h.汽车驶至停车线时立即制动后滑行的距离是s0=6m,道口宽度s=26m,汽车长l=18m.若道口栏木关闭时间t1=15s,为保障安全需要多加时间t2=20s,问此时该汽车至少要以多大的速度才能安全通过道口?