题目内容
 “塔吊”是建筑工地上普遍使用的一种起重设备,如图是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动.已知OE=10m,OC=15m,(不计“水平臂”和滑轮重力)
“塔吊”是建筑工地上普遍使用的一种起重设备,如图是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在O、D之间移动.已知OE=10m,OC=15m,(不计“水平臂”和滑轮重力)(1)由杠杆的平衡条件可知,起重机的起重量随起吊幅度而变化,起吊幅度越大,起重量
越小
越小
(2)若在C点用此塔吊能起吊重物的最大重量是1.5×104N,则配重体的重量应为多少N.
(3)当滑轮移到D点时能够安全起吊重物的最大重量是9000N,则吊臂OD的长度是多少?
分析:(1)因动力臂及动力的乘积不变,则由杠杆的平衡条件可知起吊辐度与起重量的关系;
(2)在C点用此塔吊能起重物时,知道两边力臂和在C点用此塔吊能起吊的最大重物,利用杠杆平衡条件求配重体的重量;
(3)在D点用此塔吊能起重物时,知道配重体的重量、力臂和能够安全起吊重物的最大重量,利用杠杆平衡条件即可求出吊臂OD的长度.
(2)在C点用此塔吊能起重物时,知道两边力臂和在C点用此塔吊能起吊的最大重物,利用杠杆平衡条件求配重体的重量;
(3)在D点用此塔吊能起重物时,知道配重体的重量、力臂和能够安全起吊重物的最大重量,利用杠杆平衡条件即可求出吊臂OD的长度.
解答:解:(1)由杠杆的平衡条件F1L1=F2L2(动力×动力臂=阻力×阻力臂)可知,当动力与动力臂不变时,阻力与阻力臂成反比;即阻力臂越大,阻力越小;阻力臂越小,阻力越大.而本题中的动力与动力臂都不变,则起吊幅度越大,起吊重量越小;
(2)在C点用此塔吊能起重物时,
∵GE×OE=GC×OC,
即:GE×10m=1.5×104N×15m,
GE=2.25×104N;
(2)在D点用此塔吊能起重物的最大重量是9000N时,吊臂OD的长度,
∵GE×OE=GD×OD,
即:2.25×104N×10m=9000N×OD,
OD=25.
答:(1)越小;
(2)配重体的重量应为2.25×104N;
(3)吊臂OD的长度是25m.
(2)在C点用此塔吊能起重物时,
∵GE×OE=GC×OC,
即:GE×10m=1.5×104N×15m,
GE=2.25×104N;
(2)在D点用此塔吊能起重物的最大重量是9000N时,吊臂OD的长度,
∵GE×OE=GD×OD,
即:2.25×104N×10m=9000N×OD,
OD=25.
答:(1)越小;
(2)配重体的重量应为2.25×104N;
(3)吊臂OD的长度是25m.
点评:本题考查了学生对杠杆平衡条件的掌握和运用,确定不同情况下的力与力臂的关系是正确解答本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 40、“塔吊”是建筑工地上普遍使用的起重设备.如图所示的“塔吊”,AB是竖直支架,CD是水平臂,其上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦不计.
40、“塔吊”是建筑工地上普遍使用的起重设备.如图所示的“塔吊”,AB是竖直支架,CD是水平臂,其上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦不计.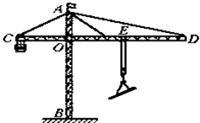 “塔吊”是建筑工地上普遍使用的起重设备.如图20中的“塔吊”,AB是竖直支架,CD是水平臂,期上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦忽略不计.OE=15m时,若用此“塔吊”能起吊重物的最大物重是8000N,求配重体有多重?当滑轮组移到D点(OD=25m)时能够安全起吊重物的最大重量是多少?(OC=10m)
“塔吊”是建筑工地上普遍使用的起重设备.如图20中的“塔吊”,AB是竖直支架,CD是水平臂,期上OC段叫平衡臂,C端装有配重体,OD段叫吊臂,E处装有滑轮组,可在O、D两点间移动,滑轮组重力及摩擦忽略不计.OE=15m时,若用此“塔吊”能起吊重物的最大物重是8000N,求配重体有多重?当滑轮组移到D点(OD=25m)时能够安全起吊重物的最大重量是多少?(OC=10m) (2011?泸州)“塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在)O、D之间移动.已知OE=10m,OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是1.5×103Kg,则配重体的质量应为
(2011?泸州)“塔吊”是建筑工地上普遍使用的一种起重设备,如图所示是“塔吊”的简化图.OB是竖直支架,ED是水平臂,OE段叫平衡臂,E端装有配重体,OD段叫吊臂,C处装有滑轮,可以在)O、D之间移动.已知OE=10m,OC=15m,CD=10m,若在C点用此塔吊能起吊重物的最大质量是1.5×103Kg,则配重体的质量应为 “塔吊”是建筑工地上普遍使用的起重设备. 如图中的“塔吊”将8000N的钢材先竖直匀速向上吊起8m,在此上升过程中,塔吊对钢材所做的功W1=
“塔吊”是建筑工地上普遍使用的起重设备. 如图中的“塔吊”将8000N的钢材先竖直匀速向上吊起8m,在此上升过程中,塔吊对钢材所做的功W1=