题目内容
两支队伍同时从相距为s的A、B两点出发,他们以同样大小的速度v相向而行.出发时,一个传令兵开始驾车以速度4v不停地往返于两支队伍的队首之间传达命令,当两支队伍相遇时,传令兵行驶的总路程为
- A.1s
- B.4s
- C.2s
- D.O
C
分析:两支队伍从相距s的两个地方,沿直线相向行驶,从两个队伍起步的那一瞬间,传令兵开始驾车行驶.我们不管传令兵按什么路径行驶,行驶的时间就是两队伍从起步到相遇的时间,知道传令兵的速度,利用速度公式求传令兵行驶的总路程.
解答:
两支队伍从相向行走到相遇的时间
t=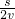 ,
,
由题知,传令兵行驶的时间等于两支队伍相遇的时间,
所以传令兵行驶的时间t=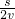 .
.
传令兵行驶的总路程:
s=v′t=4v×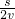 =2s.
=2s.
故选B.
点评:本题考查了速度公式的应用,解题关键是要读懂并理解题目的意思,注意传令兵行驶的时间等于两支队伍相遇的时间.
分析:两支队伍从相距s的两个地方,沿直线相向行驶,从两个队伍起步的那一瞬间,传令兵开始驾车行驶.我们不管传令兵按什么路径行驶,行驶的时间就是两队伍从起步到相遇的时间,知道传令兵的速度,利用速度公式求传令兵行驶的总路程.
解答:
两支队伍从相向行走到相遇的时间
t=
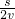 ,
,由题知,传令兵行驶的时间等于两支队伍相遇的时间,
所以传令兵行驶的时间t=
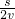 .
.传令兵行驶的总路程:
s=v′t=4v×
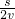 =2s.
=2s.故选B.
点评:本题考查了速度公式的应用,解题关键是要读懂并理解题目的意思,注意传令兵行驶的时间等于两支队伍相遇的时间.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目