Question

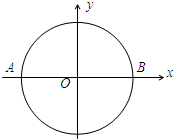如图，xOy平面内有一以原点O为圆心的圆，动点P在圆周上沿顺时针方向做速度大小始终为v的圆周运动，另一动点Q沿x轴正方向做匀速直线运动．A、B为圆与x轴的交点，某时刻P、Q在A点相遇，经过一段时间后又在B点相遇，则Q的速度大小为________．

Answer 1

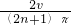（n=0，1，2…）
分析：从A点到B点，Q做匀速直线运动，P做匀速圆周运动，它们两次相遇之间所用的时间是相同的．只是P经过的路程可能是圆的周长的一半，也可能是多转了整数周后又转回来．因此，在计算结果时要考虑到这一点．
解答：Q沿直线经过的路程为2r，设速度为v′，则所用时间为t=；
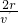P沿圆周运动，设它经过的整数圆数为n，则它经过的路程为πr+2nπr，所用的时间为t=；
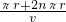因为时间t相同，所以得到方程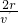=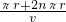，移项，合并同类项得，v′=．
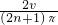n为P点运动的周数，应取整数．
故答案为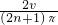：（n=0，1，2…）．
点评：解决此题的关键，是能熟练运用速度的计算公式，找出两个点运动的等量关系，根据题意列出方程，再求解．