题目内容
16.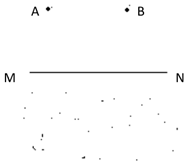 在野外生存训练中,小军的任务是要从A处走到河岸取水后然后送到B处,如图.若A、B两地相距3000m,MN是与AB连线平行的小河的河岸.AB到河岸的垂直距离为2000m,小军速度大小恒为5km/h,不考虑取水停留时间,请为小军设计一条最路线,在图中做出这条最短路线(请保留必要的作图痕迹)并算出小军取水的最短时间.
在野外生存训练中,小军的任务是要从A处走到河岸取水后然后送到B处,如图.若A、B两地相距3000m,MN是与AB连线平行的小河的河岸.AB到河岸的垂直距离为2000m,小军速度大小恒为5km/h,不考虑取水停留时间,请为小军设计一条最路线,在图中做出这条最短路线(请保留必要的作图痕迹)并算出小军取水的最短时间.
分析 (1)利用平面镜成像的特点:像与物关于平面镜对称,作出发光点A的像点A′,根据反射光线反向延长通过像点,可以由像点和B点确定反射光线所在的直线,两点之间,直线最短.
(2)已知AB间的距离是3000m,AB到河岸的距离(AD)是2000m,可以计算出DB间的距离,此时便可知道小军要走的路程了,又知速度,根据v=$\frac{s}{t}$变形计算出所需时间;
解答 解:(1)作出发光点A关于平面镜的对称点,即为像点A′,连接A′、B点交平面镜于点O,沿OB画出反射光线,连接AO画出入射光线,如图所示,图中O就是入射点;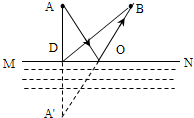
①由图可知,A′B的连线是线段,两点之间,线段最短,即此时A′B之间的距离(A′O+OB)最短;
②根据平面镜成像的特点可知,此时AD=A′D,且Rt△ADO与Rt△A′DO有一条公共边DO,故可知Rt△ADO≌Rt△A′DO,
即AO=A′O;
故AO+OB=A′O+OB;
即此时O点是最短路线的取水点.
(2)由上图可知,小军通过的路程是AO+OB,
此时,AB=3000m,AD=2000m,AA′=AD+DA′=2000m+2000m=4000m,
根据勾股定理可知,A′B=5000m,OB=$\frac{1}{2}$A′B=$\frac{1}{2}$×5000m=2500m,
DO=$\frac{1}{2}$AB=$\frac{1}{2}$×3000m=1500m,
AO=$\sqrt{(AD)^{2}+(DO)^{2}}$=$\sqrt{(2000m)^{2}+(1500m)^{2}}$=2500m,
故小军通过的路程s=AO+OB=2500m+2500m=5000m=5km,
由v=$\frac{s}{t}$可得,
所需的时间:
t=$\frac{s}{v}$=$\frac{5km}{5km/h}$=1h;
答:小军取水的最短时间为1h.
点评 本题利用平面镜成像的特点,并结合数学知识,解决实际问题(取水路线最短),综合性较强,是中考考查的热点问题.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案| A. | 质量 | B. | 温度 | C. | 比热容 | D. | 速度 |
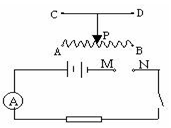 小芳同学在探究“决定导体电阻大小的因素”时,做出了如下猜想:
小芳同学在探究“决定导体电阻大小的因素”时,做出了如下猜想:猜想①:在温度不变时,导体的电阻与导体的材料有关;
猜想②:在温度不变时,导体的电阻与导体的长度有关;
猜想③:在温度不变时,导体的电阻与导体的横截面积有关.
供她选择的导体如下表所示:
| 序号 | 材料 | 长度(m) | 横截面积(mm2) |
| A | 镍铬合金 | 0.8 | 0.5 |
| B | 锰铜 | 0.4 | 1 |
| C | 锰铜 | 0.8 | 0.5 |
| D | 锰铜 | 1.2 | 0.5 |
(2)实验证明她的猜想②是正确的.于是她根据原理制作了滑动变阻器,滑动变阻器上面标的“200Ω 2A”的物理意义分别是200Ω表示滑动变阻器的最大电阻是200Ω和2A表示滑动变阻器允许通过的最大电流是2A
(3)如果一个同学制作滑动变阻器,并且在连接好电路后,闭合开关,发现怎么样移动滑片P,都不能改变灯的亮度,你觉得可能的原因是什么?变阻器都选最上面或最下面两个接线柱造成的
(4)当B接M,D接N时,滑片向左移,电流表示数将变小.
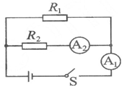 如图所示的电路中,电阻R1的阻值为10Ω.闭合开关S,电流表A1的示数为2A,电流表A2的示数为0.8A,则电阻R2的阻值为15Ω.电路中的总电阻为6Ω.
如图所示的电路中,电阻R1的阻值为10Ω.闭合开关S,电流表A1的示数为2A,电流表A2的示数为0.8A,则电阻R2的阻值为15Ω.电路中的总电阻为6Ω.

 如图为高速公路ETC电子收费通知,ETC系统采用的是一种短程无线通信方式,它通过接收车载IC卡中的感应天线发射的电磁波(选填“电磁波”或“超声波”)来收录信息.
如图为高速公路ETC电子收费通知,ETC系统采用的是一种短程无线通信方式,它通过接收车载IC卡中的感应天线发射的电磁波(选填“电磁波”或“超声波”)来收录信息.