题目内容
 某人站在离公路垂直距离为60米的A点,发现公路上有一汽车从B点以10米/秒的速度沿着公路匀速行驶,B点与人相距100米,如图所示.问此人最少要以大的速度奔跑,才能与汽车相遇?
某人站在离公路垂直距离为60米的A点,发现公路上有一汽车从B点以10米/秒的速度沿着公路匀速行驶,B点与人相距100米,如图所示.问此人最少要以大的速度奔跑,才能与汽车相遇?
解:
因为车的速度为10m/s,又因为BO长80m,所以汽车用时tBO= =8s,
=8s,
在Rt△OAC中,SOC=v车(t-8s),设相遇时间为t,则
[10m/s(t-8s)]2+(60m)2=(vt)2,
即:(t-8s)2+(60m)2=( )2,
)2,
设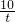 =x,则
=x,则
( )2=(
)2=(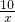 -8s)2+(60m)2,
-8s)2+(60m)2,
化简得:
v2=100x2-160x+100=100(x2-1.6x+1)=100×[(x-0.8)2+0.36],
由此可知x=0.8时,速度v最小,此时v2=100×[(0.8-0.8)2+0.36]=36,
所以v=6m/s.
答:此人最少要以6m/s的速度奔跑,才能与汽车相遇.
分析:由图知,他们在O点的右边相遇最近,设在C点相遇,相遇时间为t,在Rt△OAC中,列方程求解.
点评:本题考查了学生对速度公式掌握和运用,假设他们在O点的右边相遇是本题的关键.

因为车的速度为10m/s,又因为BO长80m,所以汽车用时tBO=
 =8s,
=8s,在Rt△OAC中,SOC=v车(t-8s),设相遇时间为t,则
[10m/s(t-8s)]2+(60m)2=(vt)2,
即:(t-8s)2+(60m)2=(
 )2,
)2,设
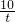 =x,则
=x,则(
 )2=(
)2=(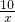 -8s)2+(60m)2,
-8s)2+(60m)2,化简得:
v2=100x2-160x+100=100(x2-1.6x+1)=100×[(x-0.8)2+0.36],
由此可知x=0.8时,速度v最小,此时v2=100×[(0.8-0.8)2+0.36]=36,
所以v=6m/s.
答:此人最少要以6m/s的速度奔跑,才能与汽车相遇.
分析:由图知,他们在O点的右边相遇最近,设在C点相遇,相遇时间为t,在Rt△OAC中,列方程求解.
点评:本题考查了学生对速度公式掌握和运用,假设他们在O点的右边相遇是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某人站在离公路垂直距离为60米的A点,发现公路上有一汽车从B点以10米/秒的速度沿着公路匀速行驶,B点与人相距100米,如图所示.问此人最少要以大的速度奔跑,才能与汽车相遇?
某人站在离公路垂直距离为60米的A点,发现公路上有一汽车从B点以10米/秒的速度沿着公路匀速行驶,B点与人相距100米,如图所示.问此人最少要以大的速度奔跑,才能与汽车相遇?

