题目内容
 如图所示,将电阻为R的均匀裸导线首尾相接形成一个半径为r的导体圆环,环上放着两根电阻不计的足够长的平行直导线a、b,相距等于圆半径r.现让直导线a、b在环面上移动,移动过程中a、b导线始终保持相互平行且距离为r,并始终与导体环有很好的接触,则在a、b移动的过程中两直导线间电阻的最大值Rmax=
如图所示,将电阻为R的均匀裸导线首尾相接形成一个半径为r的导体圆环,环上放着两根电阻不计的足够长的平行直导线a、b,相距等于圆半径r.现让直导线a、b在环面上移动,移动过程中a、b导线始终保持相互平行且距离为r,并始终与导体环有很好的接触,则在a、b移动的过程中两直导线间电阻的最大值Rmax=分析:根据导线的电阻为零可知两导轨外侧的两个弧可以剪掉了,然后分析内侧两弧并联,再判断出两弧的长度的取值范围为
圆周到
圆周即可求出a、b间电阻最小值与最大值.
| 1 |
| 6 |
| 1 |
| 4 |
解答:解:当两根导线分别位于中间位置及与圆相切的位置时,内侧弧的长度最大,即
圆周,此时a、b间电阻值最大,即
×
R=
R;
当两根导线分别距圆心为
r时,内侧弧的长度最小,即
圆周,此时a、b间电阻值最小,即
×
R=
R.
故答案为:
R;
R.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
当两根导线分别距圆心为
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
故答案为:
| 1 |
| 8 |
| 1 |
| 12 |
点评:本题考查电阻的并联,但是难度较大,重点是能够分析出两导轨外侧的两个弧被短路,然后根据导线移动的位置确定出内侧两弧的长度的取值范围.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 (2008?昌平区二模)如图所示的电路中,R为滑动变阻器,R1、R2为定值电阻,且R1>R2,E为电压恒定的电源,当滑动变阻器的滑片滑动时,通过R、R1、R2的电流将发生变化,电流变化值分别为△I、△I1、△I2表示,则( )
(2008?昌平区二模)如图所示的电路中,R为滑动变阻器,R1、R2为定值电阻,且R1>R2,E为电压恒定的电源,当滑动变阻器的滑片滑动时,通过R、R1、R2的电流将发生变化,电流变化值分别为△I、△I1、△I2表示,则( )
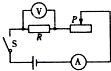 在探究“电流与电阻的关系”实验中,电路如图所示,其中定值R有R1=5Ω、R2=10Ω、R3=15Ω三种规格备用.
在探究“电流与电阻的关系”实验中,电路如图所示,其中定值R有R1=5Ω、R2=10Ω、R3=15Ω三种规格备用. 如图所示,将电阻为R的均匀裸导线首尾相接形成一个半径为r的导体圆环,环上放着两根电阻不计的足够长的平行直导线a、b,相距等于圆半径r.现让直导线a、b在环面上移动,移动过程中a、b导线始终保持相互平行且距离为r,并始终与导体环有很好的接触,则在a、b移动的过程中两直导线间电阻的最大值Rmax=________,最小值Rmin=________.
如图所示,将电阻为R的均匀裸导线首尾相接形成一个半径为r的导体圆环,环上放着两根电阻不计的足够长的平行直导线a、b,相距等于圆半径r.现让直导线a、b在环面上移动,移动过程中a、b导线始终保持相互平行且距离为r,并始终与导体环有很好的接触,则在a、b移动的过程中两直导线间电阻的最大值Rmax=________,最小值Rmin=________.