题目内容
如图(a),圆柱形容器中装入一定量的水,将一长方体木块B放置水中,上面加一长方体的金属块A,木块静止时,露出水面的高度为h1,如图(b):然后将金属块用细线悬挂在木块下面.静止时木块露出水面的高度为h2,如图(c):再将细线剪断,金属块沉入水底,当木块再次静止时露出水面的高度为h3,如图(d).

(1)若(b)(c)(d)容器中底部受到水的压强分别标记为P1、P2、P3,试写出P1、P2、P3的大小关系:______;
(2)试推导金属块A的密度.(水的密度记为ρ水)
解:(1)图(b)(c)中把A、B看做一个整体,它们都漂浮,所以浮力都等于自身的总重力;(d)图中A下沉,所以A、B受到的总浮力小于它们自身的总重力.
∴F浮b=F浮c>F浮d,
根据F浮=ρ水gV排,知V排b=V排c>V排d,
容器底面积相同,∴放入A、B后液面上升的高度△hb=△hc>△hd,
∴水深hb=hc>hd,
根据液体压强公式P=ρgh知P1=P2>P3.
(2)设B底面积为S,高为h,A的体积为V,密度为ρA,
由(b)图所示可得ρ水S(h-h1)=mA+mB…①;
由(c)图可得ρ水VA+ρS(h-h2)=mA+mB…②;
由(d)图可得ρ水S(h-h3)=mB…③,
由①-③得mA=ρ水S(h3-h1);
由①-②得VA=S(h2-h1);
则金属球的密度 ρA=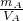 =
= =
= ρ水.
ρ水.
故答案为:P1=P2>P3; ρ水.
ρ水.
分析:(1)根据阿基米德原理及浮沉条件可知(b)(c)(d)容器中排开的液体体积大小关系,即能确定水面上升高度的大小关系,再根据液体压强公式P=ρgh可知
容器中底部受到水的压强的大小关系;
(2)根据物体的浮沉条件及阿基米德原理分别列出甲、乙、丙三图的关系式,三式联立求得金属球的质量和体积表达式,再利用ρ= 即可求得金属球的密度.
即可求得金属球的密度.
点评:此题主要综合考查物体浮沉条件的应用、压强和密度公式的计算,解答此题的关键是分别列出(b)(c)(d)三图的关系式,尤其是(d)图,不要再分析A排开的体积和受到的浮力情况,只分析空心金属盒的受到浮力情况列出等式即可.
∴F浮b=F浮c>F浮d,
根据F浮=ρ水gV排,知V排b=V排c>V排d,
容器底面积相同,∴放入A、B后液面上升的高度△hb=△hc>△hd,
∴水深hb=hc>hd,
根据液体压强公式P=ρgh知P1=P2>P3.
(2)设B底面积为S,高为h,A的体积为V,密度为ρA,
由(b)图所示可得ρ水S(h-h1)=mA+mB…①;
由(c)图可得ρ水VA+ρS(h-h2)=mA+mB…②;
由(d)图可得ρ水S(h-h3)=mB…③,
由①-③得mA=ρ水S(h3-h1);
由①-②得VA=S(h2-h1);
则金属球的密度 ρA=
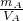 =
= =
= ρ水.
ρ水.故答案为:P1=P2>P3;
 ρ水.
ρ水.分析:(1)根据阿基米德原理及浮沉条件可知(b)(c)(d)容器中排开的液体体积大小关系,即能确定水面上升高度的大小关系,再根据液体压强公式P=ρgh可知
容器中底部受到水的压强的大小关系;
(2)根据物体的浮沉条件及阿基米德原理分别列出甲、乙、丙三图的关系式,三式联立求得金属球的质量和体积表达式,再利用ρ=
 即可求得金属球的密度.
即可求得金属球的密度.点评:此题主要综合考查物体浮沉条件的应用、压强和密度公式的计算,解答此题的关键是分别列出(b)(c)(d)三图的关系式,尤其是(d)图,不要再分析A排开的体积和受到的浮力情况,只分析空心金属盒的受到浮力情况列出等式即可.

练习册系列答案
相关题目

 如图所示,有两圆柱形容器底面积之比2:3,装有质量不等的水.将密度为0.6×103千克/米3的木块甲放入A容器中,将物块乙浸没在B容器的水中,且均不溢出,要求:水对容器底部压强变化量相等,则判断甲、乙的体积关系( )
如图所示,有两圆柱形容器底面积之比2:3,装有质量不等的水.将密度为0.6×103千克/米3的木块甲放入A容器中,将物块乙浸没在B容器的水中,且均不溢出,要求:水对容器底部压强变化量相等,则判断甲、乙的体积关系( )

