题目内容
如图所示，均匀圆环电阻R0=8欧，电压恒定为6伏，定值电阻R=1欧．导电滑臂OA的电阻不计，可以在圆环上无摩擦地滑动．电路中可以产生的最小电功率为12
12
瓦．分析：由电路图可知，圆环中上部分圆弧电阻和下部分圆弧电阻并联，然后与R串联；
电源电压一定，由P=
可知电路电阻最大时，电路功率最小，根据串并联电路的电阻规律电路的最大电阻，
然由电功率公式P=
求出电路最小电功率．
电源电压一定，由P=
| U2 |
| R |
然由电功率公式P=
| U2 |
| R |
解答：解：由电路图可知，圆环中上部分圆弧电阻R1和下部分圆弧电阻R2并联，然后与R串联；
当圆环的并联电阻最大时，电路总电阻最大，电路电功率最小，
因为R1和R2并联，且R1+R2=8Ω，当R1=R2=4Ω时，圆环并联电阻最大，
最大阻值为R环=
=
=2Ω，
电路的最小电功率P=
=
=12W．
故答案为：12．
当圆环的并联电阻最大时，电路总电阻最大，电路电功率最小，
因为R1和R2并联，且R1+R2=8Ω，当R1=R2=4Ω时，圆环并联电阻最大，
最大阻值为R环=
| R1R2 |
| R1+R2 |
| 4Ω×4Ω |
| 4Ω+4Ω |
电路的最小电功率P=
| U2 |
| R+R环 |
| (6V)2 |
| 1Ω+2Ω |
故答案为：12．
点评：本题考查了欧姆定律电功率公式的灵活运用，关键是会判断电路的连接方式，难点是求出圆环的并联电阻的最大值．
练习册系列答案
相关题目
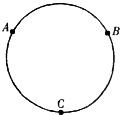如图所示的圆环是由阻值R、粗细均匀的金属丝制成的．A、B、C三点将圆环分成三等份（每等份电阻为
如图所示，将一粗细均匀，阻值为R的电阻丝弯成一圆环，A、B、C三点将圆环三等分，求A、B两点间的电阻值．
如图所示的圆环是由阻值粗细均匀的金属丝制成的．A、B、C三点将圆环分成三等份（每等份电阻为R），若将其中任意两点连入电路，则连入电路的电阻值为