题目内容
一个边长为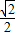 m,质量为5Kg的正方形木块,放在水平地面上,要使其绕某一点在地面上翻转过来,最省力时所需的推力为 N,用此种方法使木块竖起时,推力对其做功 J.(g取10N/kg)
m,质量为5Kg的正方形木块,放在水平地面上,要使其绕某一点在地面上翻转过来,最省力时所需的推力为 N,用此种方法使木块竖起时,推力对其做功 J.(g取10N/kg)
【答案】分析:(1)推正方体时,正方体是一个变形的杠杆,要使力最小,就要使力臂最长,用正方体的对角线作力臂,动力施加在B点.正方体的重力为阻力,OC是阻力臂.根据杠杆平衡条件,求出最小的力.
(2)要使正方体翻转一次,至少把正方体的重心从M点升高到M'点.把重为G的正方体升高OM'-OM段,由力和距离求出至少做的功.
解答: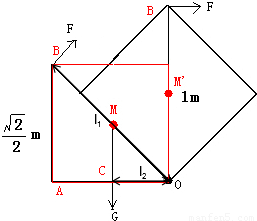 解:(1)在B端施加F方向的最小力能使正方体翻转,根据杠杆平衡条件得,
解:(1)在B端施加F方向的最小力能使正方体翻转,根据杠杆平衡条件得,
OC×G=OB×F,
边长L为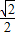 m,OB是正方体的对角线,
m,OB是正方体的对角线,
所以OB=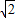 L=
L=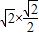 =1m.
=1m.
所以, ×
×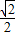 m×5kg×10N/kg=1m×F,
m×5kg×10N/kg=1m×F,
所以把此正方体翻转的最小推力为:F=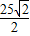 N.
N.
(2)用此种方法使木块竖起时,至少把正方体的重心从M点升高到M'点,
克服重力做功:W=Gh=5kg×10N/kg×( ×1-
×1- ×
×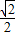 )m=
)m=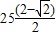 J.
J.
故答案为: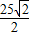 ;
;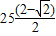 .
.
点评:本题主要考查了杠杆的最小力的问题和功的计算,本题确定最长力臂和升高的距离是关键.
(2)要使正方体翻转一次,至少把正方体的重心从M点升高到M'点.把重为G的正方体升高OM'-OM段,由力和距离求出至少做的功.
解答:
 解:(1)在B端施加F方向的最小力能使正方体翻转,根据杠杆平衡条件得,
解:(1)在B端施加F方向的最小力能使正方体翻转,根据杠杆平衡条件得,OC×G=OB×F,
边长L为
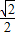 m,OB是正方体的对角线,
m,OB是正方体的对角线,所以OB=
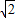 L=
L=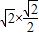 =1m.
=1m.所以,
 ×
×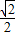 m×5kg×10N/kg=1m×F,
m×5kg×10N/kg=1m×F,所以把此正方体翻转的最小推力为:F=
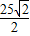 N.
N.(2)用此种方法使木块竖起时,至少把正方体的重心从M点升高到M'点,
克服重力做功:W=Gh=5kg×10N/kg×(
 ×1-
×1- ×
×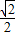 )m=
)m=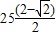 J.
J.故答案为:
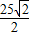 ;
;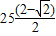 .
.点评:本题主要考查了杠杆的最小力的问题和功的计算,本题确定最长力臂和升高的距离是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 小雨使用如图所示的滑轮组提升一个边长为a、密度为ρ的立方体金属块.求:
小雨使用如图所示的滑轮组提升一个边长为a、密度为ρ的立方体金属块.求: 某同学用一根粗细均匀的铁棒,将一个边长为a的正方形重物箱撬起一个很小的角度(如图所示,图中的角度已被放大).已知:铁棒单位长度的质量为m,在另一端施加一个向上的力撬动重物箱.如果插入的长度为箱宽的五分之一,并保持该长度不变,求:
某同学用一根粗细均匀的铁棒,将一个边长为a的正方形重物箱撬起一个很小的角度(如图所示,图中的角度已被放大).已知:铁棒单位长度的质量为m,在另一端施加一个向上的力撬动重物箱.如果插入的长度为箱宽的五分之一,并保持该长度不变,求: m,质量为5Kg的正方形木块,放在水平地面上,要使其绕某一点在地面上翻转过来,最省力时所需的推力为________N,用此种方法使木块竖起时,推力对其做功________J.(g取10N/kg)
m,质量为5Kg的正方形木块,放在水平地面上,要使其绕某一点在地面上翻转过来,最省力时所需的推力为________N,用此种方法使木块竖起时,推力对其做功________J.(g取10N/kg) m,质量为5Kg的正方形木块,放在水平地面上,要使其绕某一点在地面上翻转过来,最省力时所需的推力为________N,用此种方法使木块竖起时,推力对其做功_________________J.(g取10N/kg)
m,质量为5Kg的正方形木块,放在水平地面上,要使其绕某一点在地面上翻转过来,最省力时所需的推力为________N,用此种方法使木块竖起时,推力对其做功_________________J.(g取10N/kg)