方程
x-
=1，去分母得（ ）
| 1 |
| 2 |
| x-5 |
| 3 |
| A、3x-2x+10=1 |
| B、3x-2x-10=1 |
| C、3x-2x-10=6 |
| D、3x-2x+10=6 |
下列方程是一元一次方程的是（ ）
| A、x+3y=12 | ||
| B、x2-3x=1 | ||
C、
| ||
D、
|
（1）如图，正△ABC中，点M与点N分别是BC、CA上的点，且BM=CN，连接AM、BN，两线交于点Q，求∠AQN的度数．
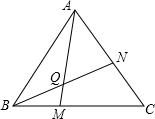
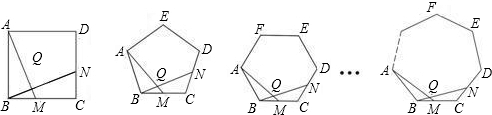
（2）将1题中的“正△ABC”分别改为正方形ABCD，正五边形ABCDE，正六边形ABCDEF，…，正n边形ABCD…N，其余条件不变，根据第1题的求解思路分别推断∠AQN的度数，将结论填入下表：
0 70774 70782 70788 70792 70798 70800 70804 70810 70812 70818 70824 70828 70830 70834 70840 70842 70848 70852 70854 70858 70860 70864 70866 70868 70869 70870 70872 70873 70874 70876 70878 70882 70884 70888 70890 70894 70900 70902 70908 70912 70914 70918 70924 70930 70932 70938 70942 70944 70950 70954 70960 70968 366461
（2）将1题中的“正△ABC”分别改为正方形ABCD，正五边形ABCDE，正六边形ABCDEF，…，正n边形ABCD…N，其余条件不变，根据第1题的求解思路分别推断∠AQN的度数，将结论填入下表：
| 正多边形 | 正方形 | 正五边形 | 正六边形 | … | 正n边形 |
| ∠AQN的度数 |
22、如图，平行四边形ABCD中，E、F分别是对角线BD上的两点，且BE=DF，连接AE、AF、CE、CF．四边形AECF是什么样的四边形，说明你的道理．