如图.已知MN是圆柱底面的直径.NP是圆柱的高.在高柱的侧面上.过点M.P嵌有一幅路径最短的金属丝.现将圆柱侧面沿NP剪开.所得的侧面展开图是( )A.B.C.D.——青夏教育精英家教网——

18、如图，已知MN是圆柱底面的直径，NP是圆柱的高，在高柱的侧面上，过点M，P嵌有一幅路径最短的金属丝，现将圆柱侧面沿NP剪开，所得的侧面展开图是（　　）

如图，是一个风筝的平面示意图，四边形ABCD是等腰梯形，E、F、G、H分别是各边的中点，假设图中阴影部分所需布料的面积为S₁，其它部分所需布料的面积之和为S₂（边缘外的布料不计），则（　　）

A、S₁＞S₂

B、S₁＜S₂

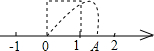如图，以数轴的单位长度为边作一个正方形，以数轴的原点为圆心，正方形对角线长为半径画弧，交数轴正半轴于点A，则点A表示的数是（　　）

14、沿着虚线将矩形剪成两部分，既能拼成三角形又能拼成梯形的是（　　）

已知两边的长分别为8，15，若要组成一个直角三角形，则第三边应该为（　　）

A、不能确定

我国南宋著名的数学家秦九韶（籍贯四川安岳）在其著书《数书九章》中，利用“三斜求积术”（即勾股定理等知识）十分巧妙地解决了“已知三角形的三边a、b、c，求其面积”的难题，而在此之前，西方数学家海伦（Heron）也解决了此问题，两者的数学公式分别是．
S=

（秦九韶），S=

p(p-a)(p-b)(p-c)

（a+b+c）（海伦）．这两个公式各有特点，若现有一个三角形，已知三边分别为5、6、7，求其面积．请你选择上面的公式，计算三角形的面积是

?ABCD中，对角线AC和BD相交于点O，若AC=6，AB=5，BD=t，则t的取值范围是

8、矩形的一个内角平分线把矩形的一条边分成长为3和5两部分，则该矩形的面积是

长、宽、高分别为3、4、5的长方体中，若最远的两个顶点是A、B，则绕其表面从顶点A到顶点B的最近“路程”是

（a≥0，b≥0）成立，则有

．请按照此性质化简使被开方数不含完全平方的因数：

0 68064 68072 68078 68082 68088 68090 68094 68100 68102 68108 68114 68118 68120 68124 68130 68132 68138 68142 68144 68148 68150 68154 68156 68158 68159 68160 68162 68163 68164 68166 68168 68172 68174 68178 68180 68184 68190 68192 68198 68202 68204 68208 68214 68220 68222 68228 68232 68234 68240 68244 68250 68258 366461