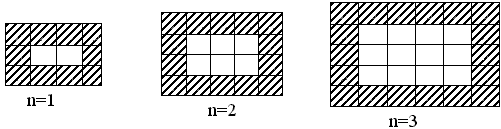
观察下列表格:
|
(1)解方程:
① 的解x= ;
的解x= ;
② 的解x= ;
的解x= ;
③ 的解x= ;
的解x= ;
④ 的解x= ;
的解x= ;
……
(2)根据你发现的规律直接写出⑤,⑥个方程及它们的解;
(3)请你用一个含正整数n的式子表示上述规律,并求出它的解。
①
 的解x= ;
的解x= ; ②
 的解x= ;
的解x= ; ③
 的解x= ;
的解x= ; ④
 的解x= ;
的解x= ;……
(2)根据你发现的规律直接写出⑤,⑥个方程及它们的解;
(3)请你用一个含正整数n的式子表示上述规律,并求出它的解。
 ,则S△A1B1C1=
,则S△A1B1C1= ;
; ,则S△A2B2C2=
,则S△A2B2C2= ;
;  ,则S△A3B3C3=
,则S△A3B3C3= ;
;  ,则S△A8B8C8=( )。
,则S△A8B8C8=( )。