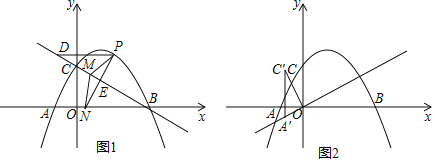【题目】二次函数y=ax2+bx+c（a，b，c为常数，且a≠0）中的x与y的部分对应值如下表：
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论：（1）ac＜0；
（2）抛物线顶点坐标为（1，5）；
（3）3是方程ax2+（b﹣1）x+c=0的一个根；
（4）当﹣1＜x＜3时，ax2+（b﹣1）x+c＞0．其中正确的序号为___________________.
【题目】重庆八中某数学兴趣小组同学探究函数
的图象与性质，根据学习函数的经验，该小组进行了系列探究．
下表给出了自变量
与函数
的一些对应值：
| … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 2 | 3 | 4 |
|
| 1 |
| … |
（1）补全表格：
，
；
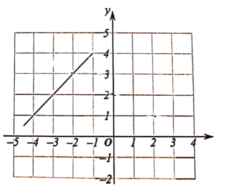
（2）在如图所示的面直角坐标系中，补全函数的图象并写出该函数的一条性质：
____________________________________________________________________________；
（3）若函数
，直接写出不等式
的解集．
【题目】近代统计学的发展起源于二十世纪初，它是在概率论的基础上发展起来的，但统计性质的工作可以追溯到远古的“结绳记事”和《二十四史》中大量的关于我国人口、钱粮、水文、天文、地震等资料的记录．现代数理统计的奠基人是英国数学家和生物学家费希尔，毕业于剑桥大学，长期在农业试验站做生物实验．费尔希在高等植物基因性状研究实验中，从若干紫花与白花中各随机抽取20株测量高度（植株正常高度
的取值范围为
），过程如下：
收集数据（单位：
）：
紫花：42，42，28，54，29，52，44，36，39，49，33，40，35，52，29，32，51，55，42，38
白花植株高度为的数据有：35，37，37，38，39，40，42，42
整理数据：
数据分为六组：
，
，
，
，
，
组别 |
|
|
|
|
|
|
紫花数量 | 3 | 2 |
| 5 | 1 | 5 |
分析数据：
植株 | 平均数 | 众数 | 中位数 | 方差 |
紫花 | 41．1 | 42 | 41 | 8．8 |
白花 | 40．25 | 43 |
| 7．2 |
应用数据：
（1）请写出表中
，
；
（2）估计500株紫花中高度正常的有多少株？
（3）结合上述数据信息，请判断哪种花长势更均匀，并说明理由（一条理由即可）．
