【题目】在平面直角坐标系中，直线与轴、轴分别交于点，，抛物线经过点，将点向右平移5个单位长度，得到点．

（1）求点的坐标；

（2）求抛物线的对称轴；

（3）若抛物线与线段恰有一个公共点，结合函数图象，求的取值范围．

．A课程成绩的频数分布直方图如下（数据分成6组：，，，，，）；

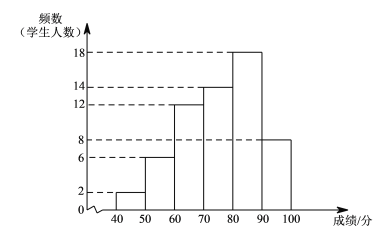
．A课程成绩在这一组是：

70 71 71 71 76 76 77 78 79 79 79

．A，B两门课程成绩的平均数、中位数、众数如下：

根据以上信息，回答下列问题：

（1）写出表中的值；

（2）在此次测试中，某学生的A课程成绩为76分，B课程成绩为71分，这名学生成绩排名更靠前的课程是________（填“A”或“B”），理由是_______；

（3）假设该年级学生都参加此次测试，估计A课程成绩超过分的人数．

【题目】如图1，在平面直角坐标系中，直线AB经过点C（a，a），且交x轴于点A（m，0），交y轴于点B（0，n），且m，n满足＋（n﹣12）2＝0．

（1）求直线AB的解析式及C点坐标；

（2）过点C作CD⊥AB交x轴于点D，请在图1中画出图形，并求D点的坐标；

（3）如图2，点E（0，﹣2），点P为射线AB上一点，且∠CEP＝45°，求点P的坐标．

【题目】如图，是与弦所围成的图形的内部的一定点，是弦上一动点，连接并延长交于点，连接．已知，设，两点间的距离为 ，，两点间的距离为，，两点间的距离为．

小腾根据学习函数的经验，分别对函数，随自变量的变化而变化的规律进行了探究．

下面是小腾的探究过程，请补充完整：

（1）按照下表中自变量的值进行取点、画图、测量，分别得到了，与的几组对应值；

（2）在同一平面直角坐标系中，描出补全后的表中各组数值所对应的点（，），（，），并画出函数，的图象；

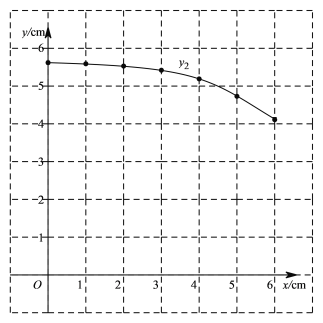
（3）结合函数图象，解决问题：当为等腰三角形时，的长度约为____．

【题目】在平面直角坐标系中，函数（）的图象经过点（4，1），直线与图象交于点，与轴交于点．

（1）求的值；

（2）横、纵坐标都是整数的点叫做整点．记图象在点，之间的部分与线段，，围成的区域（不含边界）为．

①当时，直接写出区域内的整点个数；

②若区域内恰有4个整点，结合函数图象，求的取值范围．

已知：直线及直线外一点．

求作：，使得．

作法：如图，

①在直线上取一点，作射线，以点为圆心，长为半径画弧，交的延长线于点；

②在直线上取一点（不与点重合），作射线，以点为圆心，长为半径画弧，交的延长线于点；

③作直线．

所以直线就是所求作的直线．

根据小东设计的尺规作图过程，

（1）使用直尺和圆规，补全图形；（保留作图痕迹）

（2）完成下面的证明．

证明：∵_______，_______，

∴（____________）（填推理的依据）．

（1）求证：AE＝DF．

（2）如图2，在DG上取一点M，使AG＝MG，连接CM，取CM的中点P．写出线段PD与DG之间的数量关系，并说明理由．

（3）如图3，连接CG．若CG＝BC，则AF：FB的值为　 　．

早高峰期间，乘坐_________（填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．

【题目】如图，在平面直角坐标系中，已知点其中满足：．

（1）

（2）在坐标平面内，将△ABC平移，点A的对应点为点D，点B的对应点为点E，点C的对应点为点F，若平移后E、F两点都在坐标轴上，请直接写出点E的坐标；

（3）若在△ABC内部的轴上存在一点P，在（2）的平移下，点P的对应点为点Q，使得△APQ的面积为10，则点P的坐标为_________．

(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式；

(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案；

(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值