（1）求本次测试共调查了多少名学生？

（2）求本次测试结果为B等级的学生数，并补全条形统计图；

（3）若该中学八年级共有900名学生，请你估计八年级学生中体能测试结果为D等级的学生有多少人？

【题目】如图，、、分别平分的外角、内角、外角．以下结论：①：②：③：④．其中正确的结论有（ ）

A. 1个 B. 2个 C. 3个 D. 4个

【题目】如图①，已知线段，，线段在线段上运动，、分别是、的中点.

（1）若，则______；

（2）当线段在线段上运动时，试判断的长度是否发生变化？如果不变请求出的长度，如果变化，请说明理由；

（3）我们发现角的很多规律和线段一样，如图②已知在内部转动，、分别平分和，则、和有何数量关系，请直接写出结果不需证明.

【题目】下列结论:①平面内3条直线两两相交，共有3个交点;②在平面内，若∠AOB =40°，∠AOC= ∠BOC,则∠AOC的度数为20°;③若线段AB=3, BC=2，则线段AC的长为1或5;④若∠a+∠β=180°，且∠a<∠β，则∠a的余角为(∠β-∠a).其中正确结论的个数（ ）

A.1个B.2个C.3个D.4个

【题目】如图，在平面直角坐标系中，点A（a，b）为第一象限内一点，且a＜b．连结OA，并以点A为旋转中心把OA逆时针转90°后得线段BA．若点A、B恰好都在同一反比例函数的图象上，则的值等于___．

【题目】如图，已知和都是直角，它们有公共顶点．

（1）若，求的度数．

（2）判断和的大小关系，并说明理由．

（3）猜想：和有怎样的数量关系，并说明理由．

【题目】定义符号的含义为：当时，；当时，如：，=则的最大值是______．

【题目】如图，在ABCD中，AB＝6a，BC＝6b，∠D＝60°，点E、F、G、H分别在ABCD各边上，且BE＝DG＝AE，CF＝AH＝BF．

（1）求证：四边形EFGH是平行四边形；

（2）若四边形EFGH是菱形，求的值；

（3）四边形EFGH能为正方形吗？若能，请直接写出a、b的值；若不能，请说明理由．

【题目】参照学习函数的过程与方法，探完函数y＝（x≠0）的图象与性质，因为y＝＝1﹣，即y＝﹣+1，所以我们对比函数y＝﹣来探究．

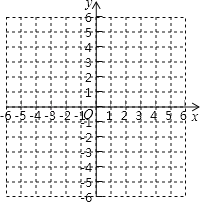
操作：面出函数y＝（x≠0）的图象．

列表：

描点：在平面直角坐标中，以自变量x的取值为横坐标，以y＝相应的函数值为纵坐标，描出如图所示相应的点；

连线：请把y轴左边和右边各点，分别用一条光滑曲线顺次连接起来．

观察：由图象可知：

①当x＞0时，y随x的增大而　 　（填“增大”或“减小”）

②y＝的图象可以由y＝﹣的图象向　 　平移　 　个单位长度得到．

③y的取值范围是　 　．

探究：①A（m1，n1），B（m2，n2）在函数y＝图象上，且n1+n2＝2，求m1+m2的值；

②若直线l对应的函数关系式为y1＝kx+b，且经过点（﹣1，3）和点（1，﹣1），y2＝，若y1＞y2，则x的取值范围为　 　．

延伸：函数y＝的图象可以由反比例函数y＝　 　的图象向　 　平移　 　个单位，再向　 　平移　 　个单位得到．