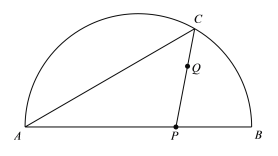
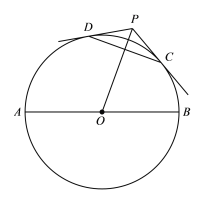
如图,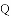
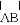 与弦
与弦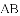
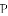
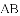
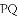
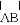 于点
于点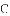
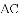
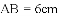
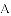
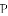
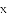
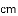
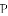
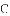
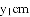 ,
,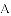
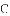
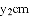 .
.
小腾根据学习函数的经验,分别对函数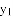 ,
,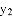 随自变量
随自变量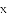
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量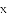
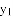 ,
,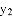 与
与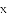
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
(2)在同一平面直角坐标系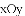
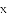
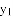 ),(
),(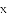
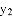 ),并画出函数
),并画出函数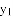 ,
,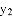 的图象;
的图象;
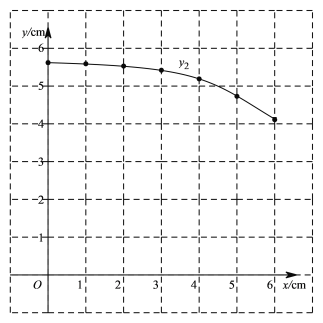
(3)结合函数图象,解决问题:当
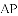
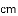
某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
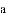
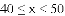
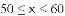
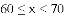
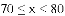
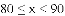
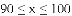
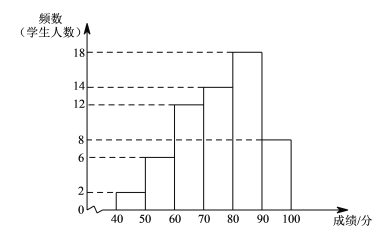
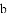
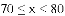
70 71 71 71 76 76 77 78 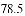
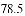
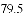
课程 | 平均数 | 中位数 | 众数 |
A |
|
|
|
B |
| 70 | 83 |
根据以上信息,回答下列问题:
(1)写出表中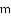
(2)在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是________(填“A”或“B”),理由是_______;
(3)假设该年级学生都参加此次测试,估计A课程成绩超过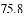
在平面直角坐标系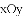
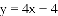
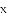
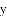
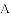
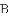
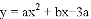 经过点
经过点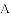
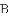
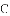
(1)求点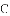
(2)求抛物线的对称轴;
(3)若抛物线与线段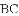
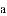
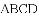


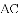
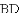
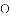
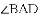
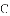
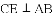
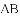
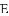
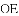
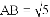 ,
,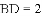
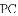
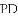
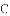
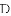
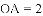
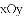
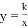 (
(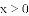
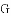
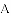
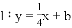 与图象
与图象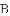
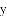
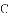
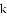
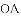
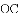
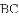
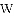
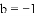
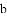
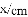
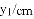
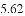
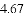
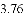
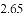
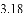
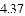
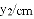
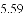
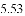
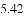
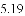
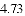
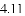
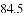
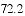
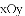
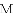
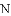
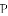
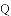
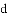
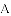
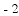
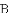
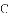
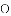
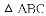
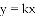
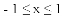
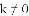
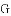
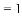
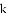

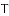
 ,-1,0,-3.2这四个数中,属于负分数的是( )
,-1,0,-3.2这四个数中,属于负分数的是( )