如图，四边形ABCD中，AD∥BC，AE⊥AD交BD于点E，CF⊥BC交BD于点F，且AE=CF，求证：四边形ABCD是平行四边形．
证明见解析.
【解析】试题分析：根据AAS可证明Rt△AED≌Rt△CFB，得到AD=BC，利用一组对边平行且相等的四边形是平行四边形可判断四边形ABCD是平行四边形.
试题解析：∵AE⊥AD，CF⊥BC，∴∠EAD=∠FCB=90°，∵AD∥BC，∴∠ADE=∠CBF，在Rt△AED和Rt△CFB中，∵，∴Rt△AED≌Rt△CFB（AAS），∴AD=BC，∵AD∥BC，∴四边形AB... 如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE.已知∠BAC＝30°，EF⊥AB，垂足为点F，连接DF.
(1)试说明AC＝EF；
(2)求证：四边形ADFE是平行四边形．
（1）证明见解析（2）证明见解析
【解析】证明：（1）∵△ABE是等边三角形，EF⊥AB，
∴∠AEF =∠AEB= 30º，AE=AB，∠EFA= 90º．
∵∠ACB= 90º，∠BAC= 30º，
∴∠EFA=∠ACB，∠AEF=∠BAC．
∴△AEF≌△BAC．
∴AC = EF．
（2）∵△ACD是等边三角形，
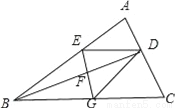
∴AC = AD，∠DAC=... 如图，BD是△ABC的角平分线，它的垂直平分线分别交AB，BD，BC于点E，F，G，连接ED，DG．
（1）请判断四边形EBGD的形状，并说明理由；
（2）若∠ABC=30°，∠C=45°，ED=2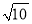
，点H是BD上的一个动点，求HG+HC的最小值．
（1）四边形EBGD是菱形，理由见解析；（2）.
【解析】试题分析：（1）四边形EBGD是菱形，根据已知条件易证△EFD≌△GFB，可得ED=BG，所以BE=ED=DG=GB，即可判定四边形EBGD是菱形．（2）作EM⊥BC于M，DN⊥BC于N，连接EC交BD于点H，此时HG+HC最小，在RT△EMC中，求出EM、MC即可解决问题．
试题解析：（1）四边形EBGD是菱形．
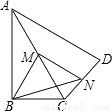
理由：... 如图，在四边形ABCD中，∠ABC=90°，AC=AD，M，N分别为AC，CD的中点，连接BM，MN，BN．
（1）求证：BM=MN；
（2）∠BAD=60°，AC平分∠BAD，AC=2，求BN的长．
（1）证明见解析；（2）
【解析】试题分析：（1）在△CAD中，由中位线定理得到MN∥AD，且MN=AD，在Rt△ABC中，因为M是AC的中点，故BM=AC，即可得到结论；
（2）由∠BAD=60°且AC平分∠BAD，得到∠BAC=∠DAC=30°，由（1）知，BM=AC=AM=MC，得到∠BMC =60°．由平行线性质得到∠NMC=∠DAC=30°，故∠BMN90°，得到，再由MN=... 我们给出如下定义：顺次连接任意一个四边形各边中点所得的四边形叫中点四边形．
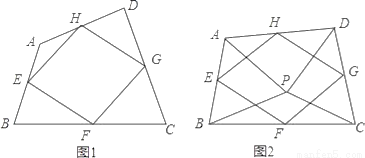
（1）如图1，四边形ABCD中，点E，F，G，H分别为边AB，BC，CD，DA的中点．求证：中点四边形EFGH是平行四边形；
（2）如图2，点P是四边形ABCD内一点，且满足PA=PB，PC=PD，∠APB=∠CPD，点E，F，G，H分别为边AB，BC，CD，DA的中点，猜想中点四边形EFGH的形状，并证明你的猜想；
（3）若改变（2）中的条件，使∠APB=∠CPD=90°，其他条件不变，直接写出中点四边形EFGH的形状．（不必证明）
（1）证明见解析；（2）四边形EFGH是菱形，证明见解析；（3）四边形EFGH是正方形.
【解析】试题分析：（1）如图1中，连接BD，根据三角形中位线定理只要证明EH∥FG，EH=FG即可．
（2）四边形EFGH是菱形．先证明△APC≌△BPD，得到AC=BD，再证明EF=FG即可．
（3）四边形EFGH是正方形，只要证明∠EHG=90°，利用△APC≌△BPD，得∠ACP=∠B... 在下列条件中，能够判定一个四边形是平行四边形的是（ ）
A. 一组对边平行，另一组对边相等
B. 一组对边相等，一组对角相等
C. 一组对边平行，一条对角线平分另一条对角线
D. 一组对边相等，一条对角线平分另一条对角线
C
【解析】A、错误．这个四边形有可能是等腰梯形．
B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．
D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
故选C． 设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是（ ）
A. a＞b B. a=b C. a＜b D. b=a+180°
B
【解析】∵四边形的内角和等于a，
∴a=（4﹣2）•180°=360°．
∵五边形的外角和等于b，
∴b=360°，
∴a=b．
故选B． 如图是一个由5张纸片拼成的平行四边形，相邻纸片之间互不重叠也无缝隙，其中两张等腰直角三角形纸片的面积都为S1，另两张直角三角形纸片的面积都为S2，中间一张正方形纸片的面积为S3，则这个平行四边形的面积一定可以表示为（ ）
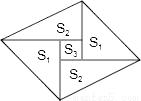
A. 4S1 B. 4S2 C. 4S2+S3 D. 3S1+4S3
A
【解析】试题分析：设等腰直角三角形的直角边长为a，中间小正方形的边长为b，则另两个直角三角形的边长分别为a-b，a+b，所以S1=，S2=，S3=，平行四边形的面积=2S1+2S2+S3=++=2=4S1，故答案选A. 在?ABCD中，AB=3，BC=4，当?ABCD的面积最大时，下列结论正确的有（ ）
①AC=5；②∠A+∠C=180°；③AC⊥BD；④AC=BD．
A. ①②③ B. ①②④ C. ②③④ D. ①③④
B
【解析】根据题意得：当?ABCD的面积最大时，四边形ABCD为矩形，
∴∠A=∠B=∠C=∠D=90°，AC=BD，
∴AC==5，
①正确，②正确，④正确；③不正确；
故选：B． 如图，在?ABCD中，AB＝6，BC＝8，∠BCD的平分线交AD于点E，交BA的延长线于点F，则AE＋AF的值等于( )
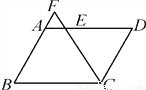
A. 2 B. 3 C. 4 D. 6
C
【解析】试题分析：由平行四边形的性质和角平分线得出∠F=∠FCB，证出BF=BC=8，同理：DE=CD=6，求出AF=BF﹣AB=2，AE=AD﹣DE=2，即可得出结果．∵四边形ABCD是平行四边形， ∴AB∥CD，AD=BC=8，CD=AB=6，
∴∠F=∠DCF，∵∠C平分线为CF，∴∠FCB=∠DCF，∴∠F=∠FCB， ∴BF=BC=8，
同理：DE=CD=6， ∴A...