下面的表格列出了一个实验的统计数据，表示将皮球从高处落下时，弹跳高度b与下降高度d的关系，下面能表示这种关系的式子是（ ）
d | 50 | 80 | 100 | 150 |
b | 25 | 40 | 50 | 75 |
A. b=d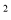
B. b=2d C. b= 
d D. b=d+25
弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的质量x（kg）间有下面的关系：
x | 0 | 1 | 2 | 3 | 4 | 5 |
y | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |
下列说法不正确的是（ ）
A. x与y都是变量，且x是自变量，y是因变量
B. 所挂物体质量为4kg时，弹簧长度为12cm
C. 弹簧不挂重物时的长度为0cm
D. 物体质量每增加1kg，弹簧长度y增加0.5cm
D 【解析】A．x与y都是变量，且x是自变量，y是因变量，故A正确； B．所挂物体质量为4kg时，弹簧长度为12cm，故B正确； C．弹簧不挂重物时的长度为10cm，故C错误； D．物体质量每增加1kg，弹簧长度y增加0.5cm，故D正确． 故选：D．某烤鸭店在确定烤鸭的烤制时间时，主要依据的是下表的数据：
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克，烤制时间为t，估计当x=3.2千克时，t的值为（ ）
A. 140 B. 138 C. 148 D. 160
C 【解析】观察表格可知，烤鸭的质量每增加0.5千克，烤制时间增加20分钟，由此可判断烤制时间是烤鸭质量的一次函数，设烤制时间为t分钟，烤鸭的质量为x千克，t与x的一次函数关系式为：t=kx+b，取（1，60），（2，100）代入，运用待定系数法求出函数关系式，再将x=3.2千克代入即可求出烤制时间t． 【解析】 从表中可以看出，烤鸭的质量每增加0.5千克，烤制的时间增加20分钟，由...在某次实验中，测得两个变量m和v之间的4组对应数据如下表：则m与v之间的关系最接近于下列各关系式中的（ ）
m | 1 | 2 | 3 | 4 |
v | 0.01 | 2.9 | 8.03 | 15.1 |
A. v=2m﹣2 B. v=m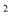
﹣1 C. v=3m﹣3 D. v=m+1
一个学习小组利用同一块木板，测量了小车从不同高度下滑的时间，他们得到如下数据：
支撑物高度h（cm） | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 |
小车下滑时间t（s） | 4.23 | 3.00 | 2.45 | 2.13 | 1.89 | 1.71 | 1.59 | 1.50 |
下列说法错误的是（ ）
A. 当h=50cm时，t=1.89s
B. 随着h逐渐升高，t逐渐变小
C. h每增加10cm，t减小1.23s
D. 随着h逐渐升高，小车的速度逐渐加快
C 【解析】A．当h=50cm时，t=1.89s，故A正确； B．随着h逐渐升高，t逐渐变小，故B正确； C．h每增加10cm，t减小的值不一定，故C错； D．随着h逐渐升高，小车的时间减少，小车的速度逐渐加快，故D正确； 故选：C．
ah，a=2cm中，下列说法正确的是（ ）