0 320758 320766 320772 320776 320782 320784 320788 320794 320796 320802 320808 320812 320814 320818 320824 320826 320832 320836 320838 320842 320844 320848 320850 320852 320853 320854 320856 320857 320858 320860 320862 320866 320868 320872 320874 320878 320884 320886 320892 320896 320898 320902 320908 320914 320916 320922 320926 320928 320934 320938 320944 320952 366461
 5(行
5(行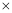 列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为
列)的数阵,是由一些连续奇数组成的,形如图框中的四个数,设第一行的第一个数为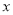 .
.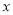 的式子表示另外三个数;
的式子表示另外三个数;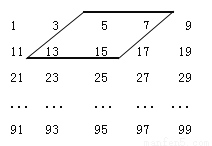
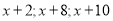 .
.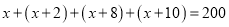 ,
,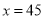 .
.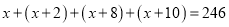 .
.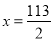 .
.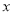 台时,两商场所需要费用一样多,根据费用一样多列出方程,解方程即可;(3)在(2)的基础上,比较即可.
台时,两商场所需要费用一样多,根据费用一样多列出方程,解方程即可;(3)在(2)的基础上,比较即可.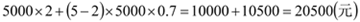
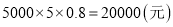 ,
,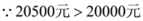 ,
,  乙商场更优惠.
乙商场更优惠.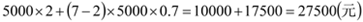 ,乙商场:
,乙商场: 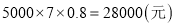 .
. 27500元<28000元,
27500元<28000元,  甲商场更优惠.
甲商场更优惠.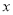 台时,两商场所需要费用一样多,根据题意得
台时,两商场所需要费用一样多,根据题意得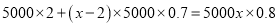 ,解得:
,解得: 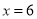 .
.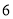 台时,两商场所需要费用一样多.
台时,两商场所需要费用一样多.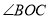 是锐角,ON平分
是锐角,ON平分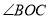 ,OM平分∠AOB.
,OM平分∠AOB.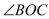 =30°,求
=30°,求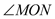 的度数?
的度数?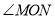 的度数;
的度数;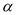 (90°≤
(90°≤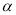 <180°),
<180°),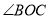 =
= 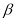 (0°<
(0°<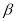 <90°),请用含有
<90°),请用含有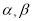 的式子直接表示上述两种情况
的式子直接表示上述两种情况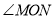 的度数.
的度数.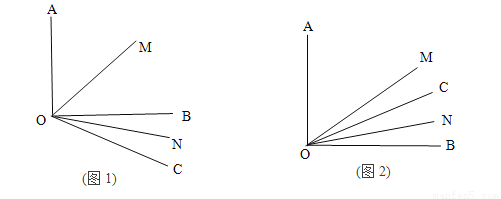
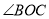 是锐角,ON平分
是锐角,ON平分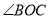 ,OM平分∠AOB.
,OM平分∠AOB.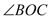 =30°,求
=30°,求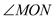 的度数?
的度数?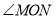 的度数;
的度数;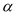 (90°≤
(90°≤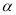 <180°),
<180°),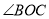 =
= 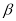 (0°<
(0°<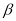 <90°),请用含有
<90°),请用含有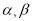 的式子直接表示上述两种情况
的式子直接表示上述两种情况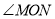 的度数.
的度数.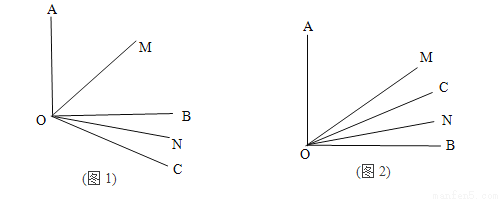
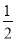 (
(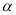 +
+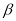 ),;②∠MON=
),;②∠MON=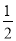 (
(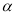 -
-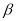 ).
).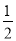 ∠AOB,∠BON=
∠AOB,∠BON=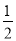 ∠BOC.
∠BOC.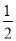 ×90°=45°,∠BON=
×90°=45°,∠BON=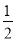 ×30°=15°,
×30°=15°,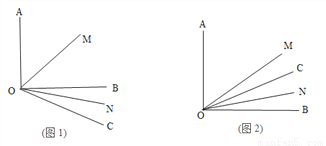
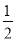 (
(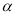 +
+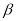 ),②∠MON=
),②∠MON=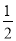 (
(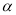 -
-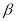 ).
).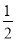 DB,E是BC的中点,BE=
DB,E是BC的中点,BE=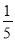 AC=2cm,求DE的长.
AC=2cm,求DE的长.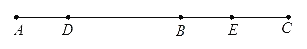
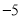 的相反数是( )
的相反数是( )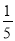 B.
B. 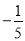 C. 5 D.
C. 5 D. 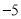
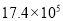 B.
B. 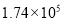 C.
C. 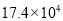 D.
D. 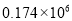
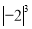 和
和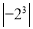
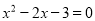 B.
B. 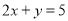 C.
C. 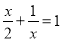 D.
D. 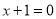
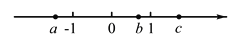
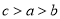 B.
B. 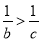
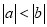 D.
D. 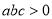
 ,则
,则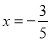 B. 若
B. 若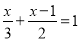 ,则
,则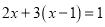
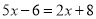 ,则
,则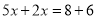 D. 若
D. 若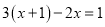 ,则
,则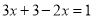
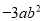 和
和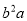 是同类项 B.
是同类项 B. 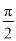 不是单项式
不是单项式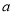 比
比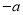 大 D. 2是方程
大 D. 2是方程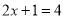 的解
的解