0 320641 320649 320655 320659 320665 320667 320671 320677 320679 320685 320691 320695 320697 320701 320707 320709 320715 320719 320721 320725 320727 320731 320733 320735 320736 320737 320739 320740 320741 320743 320745 320749 320751 320755 320757 320761 320767 320769 320775 320779 320781 320785 320791 320797 320799 320805 320809 320811 320817 320821 320827 320835 366461
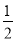 )2=0.
)2=0.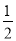 [x2﹣2(4x﹣4xy)],其中x=﹣2.
[x2﹣2(4x﹣4xy)],其中x=﹣2.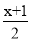 ﹣1=
﹣1=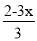 .
.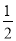 )3的值.
)3的值.
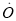 . 对于两个不同的M和N,若点M、点N到点
. 对于两个不同的M和N,若点M、点N到点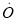 的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数
的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数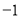 ,点N表示数3,它们与基准点
,点N表示数3,它们与基准点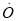 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.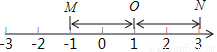
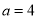 ,则b= ;
,则b= ;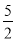 ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;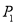 ,
, 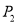 为
为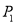 的基准变换点,点
的基准变换点,点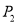 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到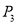 ,
, 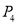 为
为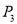 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到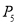 ,
, 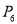 ,…,
,…, 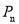 .
. 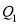 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后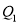 的落点为
的落点为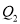 ,
, 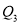 为
为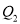 的基准变换点, 将数轴沿原点对折后
的基准变换点, 将数轴沿原点对折后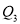 的落点为
的落点为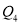 ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到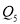 ,
, 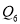 ,…,
,…, 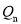 .若无论k为何值,
.若无论k为何值, 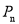 与
与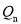 两点间的距离都是4,则n= .
两点间的距离都是4,则n= .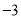 的倒数得( ).
的倒数得( ).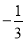 B.
B. 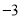 C.
C. 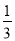 D.
D. 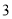
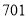 年,记作
年,记作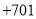 ,那么秦始皇出生于公元前
,那么秦始皇出生于公元前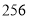 年,可记作( ).
年,可记作( ).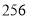 B.
B. 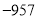 C.
C. 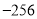 D.
D. 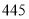
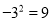 B.
B. 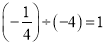 C.
C. 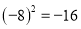 D.
D.